Процедура последовательного присоединения элементов
Переход к меньшему числу объясняющих переменных может уменьшить дублирование информации, доставляемой сильно взаимозависимыми признаками. Именно с этим мы сталкиваемся в случае мультиколлинеарности объясняющих переменных. Пусть
Тогда квадрат коэффициента
где Подправленная на несмещенность оценка
(Если по формуле (56) получают отрицательное число, то полагают Нижняя доверительная граница для
На практике, при решении вопроса о том какие объясняющие переменные следует включать в модель, часто используют процедуру последовательного присоединения элементов. 1-й шаг 2-й шаг Процедуру продолжают до тех пор, когда на шаге
Тогда в модель включают наиболее информативные переменные, полученные на первых Используют и другие методы устранения мультиколлинеарности. Рассмотрим пример 5. Имеются следующие условные данные (табл. 6). Таблица 6.
Рассмотрим влияние на зависимую переменную каждой из объясняющих переменных в отдельности. Вычисляя парные коэффициенты корреляции, получим, что наибольшее значение имеет коэффициент Рассмотрим влияние на зависимую переменную пар переменных
Затем рассмотрим влияние пары переменных
Таким образом, следует выбрать пару переменных Рассмотрим влияние на зависимую переменную трех переменных
Таким образом, следуя рекомендациям метода последовательного присоединения переменных, в уравнение следует включить все три объясняющие переменные. Однако
|

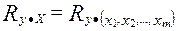 - множественный коэффициент корреляции между зависимой переменной
- множественный коэффициент корреляции между зависимой переменной 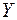 и набором объясняющих переменных
и набором объясняющих переменных  . Он определяется как обычный парный коэффициент корреляции между
. Он определяется как обычный парный коэффициент корреляции между 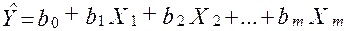 . Пусть
. Пусть  - матрица обратная к матрице
- матрица обратная к матрице  :
: (54)
(54) , (55)
, (55)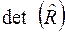 - определитель матрицы
- определитель матрицы  .
. коэффициента детерминации
коэффициента детерминации  имеет вид
имеет вид . (56)
. (56)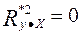 ).
).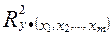 определяется по формуле
определяется по формуле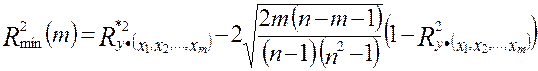 (57)
(57) . Выбирается наиболее информативная объясняющая переменная, которая максимизирует величину
. Выбирается наиболее информативная объясняющая переменная, которая максимизирует величину 
 . При этом
. При этом 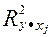 совпадает с квадратом обычного парного коэффициента корреляции
совпадает с квадратом обычного парного коэффициента корреляции  . Пусть
. Пусть  , тогда наиболее информативной будет переменная
, тогда наиболее информативной будет переменная  . Затем рассчитывают подправленный на несмещенность коэффициент
. Затем рассчитывают подправленный на несмещенность коэффициент  и его нижнюю доверительную границу
и его нижнюю доверительную границу  .
.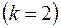 . Среди всевозможных пар объясняющих переменных
. Среди всевозможных пар объясняющих переменных 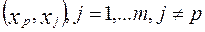 выбирается та, которая максимизирует величину
выбирается та, которая максимизирует величину  . Пусть
. Пусть  , тогда наиболее информативной будет пара
, тогда наиболее информативной будет пара 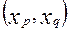 . Затем рассчитывают подправленный на несмещенность коэффициент
. Затем рассчитывают подправленный на несмещенность коэффициент 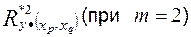 и его нижнюю доверительную границу
и его нижнюю доверительную границу 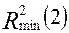 .
. выполнится условие
выполнится условие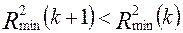 . (58)
. (58)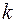 шагах. Отметим, что в расчетах используют формулы (56) и (57) в которых вместо
шагах. Отметим, что в расчетах используют формулы (56) и (57) в которых вместо 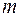 берут соответствующее значение номера шага
берут соответствующее значение номера шага 
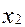

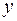
 =
= 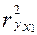 =0,602. Тогда
=0,602. Тогда 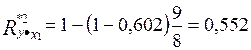 ,
,  .
.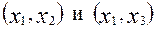 . Сначала рассмотрим влияние пары переменных
. Сначала рассмотрим влияние пары переменных 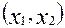 .
.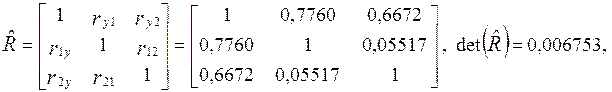
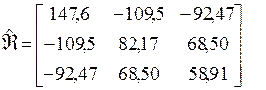 ,
,  .
. .
.
 ,
, 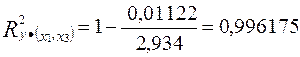 .
. ,
, 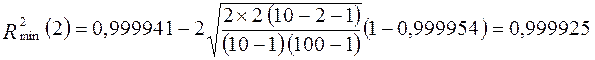 .
.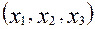 .
.

 ,
, 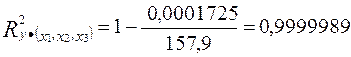 ,
, 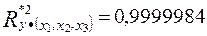 ,
, 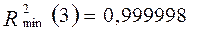 .
.
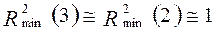 , поэтому введение в уравнение третьей переменной почти не изменяет коэффициента детерминации. Кроме того, переменные
, поэтому введение в уравнение третьей переменной почти не изменяет коэффициента детерминации. Кроме того, переменные  сильно коррелируют друг с другом, поэтому следует предпочесть модель
сильно коррелируют друг с другом, поэтому следует предпочесть модель 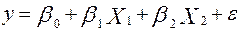 .
.


