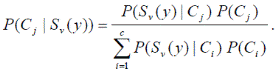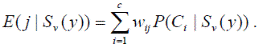Байесовское правило для последовательных процедур
При построении последовательной процедуры распознавания практически полезными оказываются Байесовские процедуры принятия решений. Для описания такой процедуры введём следующие понятия. Стоимость ошибочного распознавания wij определяется как вещественное число, представляющее стоимость распознавания образа как элемента класса Ci, в то время как на самом деле он принадлежит классу Cj. Стоимость измерения fi — вещественное число, определяющее затраты на измерение i -го признака образа. P (Ci) — вероятность того, что случайным образом выбранный объект будет принадлежать классу Ci. P (Sv (y)) — вероятность того, что описание случайно выбранного объекта удовлетворит последовательности длины v. P (Sv (y)| Cj) — вероятность того, что объект, случайно выбранный из класса Cj, удовлетворит последовательности Sv (y). P(Cj | Sv (y)) — вероятность того, что случайный объект, удовлетворяющий последовательности Sv (y), будет принадлежать классу Cj. Байесовское правило позволяет в процессе последовательного распознавания давать ответы на вопросы следующего вида: Если на определённом шаге известно, что частичное описание образа есть Sv (y), к какому классу с большей вероятностью он относится? Выведем такое правило. Совместная вероятность того, что образ удовлетворит частичному описанию Sv (y), а также того, что образ принадлежит классу Cj, равна P (Sv (y) • Cj) = P (Cj) P (Sv (y)| Cj) (5.1). Эту же вероятность можно раскрыть как P (Sv (y) • Cj) = P (Sv (y)) P(Cj | Sv (y)) (5.2). Из второй записи следует выражение для искомой вероятности:
Знаменатель в правой части есть сумма всех возможностей появления рассматриваемой последовательности, т.е. сумма вероятностей появления последовательности в каждом классе, взвешенная вероятностями появления каждого класса:
Подставляя в (5.3) в качестве числителя выражение (5.1), а в качестве знаменателя — (5.4), получим формулу Байеса для последовательной процедуры распознавания:
Ожидаемые потери, связанные с решением отнести объект, удовлетворяющий последовательности (Sv (y), к классу Cj, равны
Оптимальное правило распознавания строится таким образом, что любое принятие решения об отнесении образа к определённому классу минимизировало данную функцию потерь. С точки зрения построения последовательное правило распознавания может носить эвристический характер, т.е. конструироваться вручную на основе знаний о предметной области. Существует, однако, и формальные способы построения правила на основе процедуры обучения.
|

 (5.3)
(5.3) (5.4)
(5.4)