Прямой метод построения функций принадлежности
Лабораторная работа №1. Нечеткие модели принятия решений Каев Э. А. группа 4296 Прямой метод построения функций принадлежности Лингвистическая переменная «Размер дохода на одного члена семьи». Универсальное множество X = {5000, 6000, 7000, 8000, 9000, 10000, 11000, 12000, 13000, 14000}. Названия терм-множеств: «Малый», «Средний», «Высокий».
Нечеткая переменная №1 <Малый, {5000, 6000, 7000, 8000, 9000, 10000, 11000, 12000, 13000, 14000}, A1> Нечеткая переменная №2 <Средний, {5000, 6000, 7000, 8000, 9000, 10000, 11000, 12000, 13000, 14000}, A2> Нечеткая переменная №2 <Высокий, {5000, 6000, 7000, 8000, 9000, 10000, 11000, 12000, 13000, 14000}, A3>
В опросе участвовало 10 экспертов.
В таблице 1 указаны результаты опроса экспертов на принадлежность значений xi нечеткому понятию «Малый размер дохода». Таблица №1
Получим функцию принадлежности A1= {<1/5000>, <1/6000>, <0.8/7000>, <0.5/8000>, <0.2/9000>, <0/10000>, <0/11000>, <0/12000>, <0/13000>, <0/14000>}. В таблице 2 указаны результаты опроса экспертов на принадлежность значений xi нечеткому понятию «Средний размер дохода». Таблица №2
Получим функцию принадлежности A2= {<0/5000>, <0.2/6000>, <0.6/7000>, <0.9/8000>, <1/9000>, <0.8/10000>, <0.5/11000>, <0.1/12000>, <0/13000>, <0/14000>}.
В таблице 3 указаны результаты опроса экспертов на принадлежность значений xi нечеткому понятию «Высокий размер дохода». Таблица №3
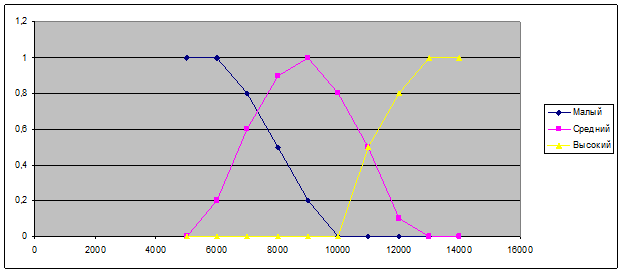
Получим функцию принадлежности A3= {<0/5000>, <0/6000>, <0/7000>, <0/8000>, <0/9000>, <0/10000>, <0.5/11000>, <0.8/12000>, <1/13000>, <1/14000>}. Полученные функции принадлежности изображены на рисунке 1.
Рис. 1. Полученные функции принадлежности
Рис. 2. Интервалы значений Интервал значений для нечеткого понятия «Малый размер дохода» = [5000, 7400] Интервал значений для нечеткого понятия «Средний размер дохода» = [8000, 11000] Интервал значений для нечеткого понятия «Высокий размер дохода» = [11000, 14000]
|