МОРФОГЕНЕЗ РАСТЕНИЙ И ПРОЦЕССЫ БИОЛОГИЧЕСКОГО ВРЕМЕНИ
Строится конкретная грубая динамическая система биологического времени растений. Рассматривается структура биологического временного поля. Часть структурной организации поля описывает деятельность меристематической ткани конуса нарастания растения. В целом, биологическое временное поле соответствует организации морфологических процессов растения. Ключевые слова: биологическое время, морфогенез, физиологические события, грубая динамическая система, клетка.
Введение. Проблема развития растений до сих пор является актуальным звеном в изучении организма растений. Причины морфогенеза представляют собой не выясненную проблему. В то же время рост и развитие растений проходит за определенный отрезок времени. Этот отрезок времени не является постоянной величиной, а изменяется в зависимости от напряженности факторов внешней среды. Поэтому является целесообразным рассматривать временные интервалы онтогенеза. Фундамент, который необходимо заложить – это так же как в физике проблемы пространства-времени. Нам необходимо рассматривать пространственно-временную организацию растительного организма. На данный момент исследований можно отметить, что до сих пор в изучении проблем растительного организма используется физическая шкала времени. Эта шкала предполагает, что время изменяется (течет) равномерно и прямолинейно. В то же время, нужно сказать о том, что исследования в области агрометеорологии показывают, что, например, длительность периода посев-созревание растений (весь период онтогенеза) имеет различную продолжительность в зависимости от состояния факторов внешней среды. Этот факт был известен в XIX веке. То есть, однозначно можно утверждать о существовании биологической оси времени. Таким образом, существуют две системы отсчета времени: физическая и биологическая. Если говорить о более высоком уровне проблемы биологического времени, то необходимо говорить о структуре, которая лежит в основе функционирования растительного организма. Такая структура определяет весь морфогенез растений, физиологические события определяются структурной организацией биологического временного поля. В неявном виде исследования структурной организации биологического временного поля проведены Л.В. Белоусовым и Б.Н. Белинцевым [1,2]. Только в этих исследованиях предполагается существование некоторого морфогенетического поля с наличием своих источников и стоков. Содержание морфогенетического поля расплывчато. Более точно можно говорить о существовании биологического временного поля, не вводя в структуру исследования новых, неясных, неизвестных науке субстанций. Таким образом, мы будем исследовать время, которое имеет структурную организацию в организме растения. Здесь предлагается совершенно конкретная грубая динамическая система биологического времени растений. Математическое понятие грубости соответствует понятию надежности биологических систем – Д.М. Гродзинский [3]. Мы покажем, что структурная организация биологического временного поля имеет свои источники и стоки. Более того, интегральные траектории биологического временного поля могут иметь структуру колебательного процесса, могут уходить в бесконечность вправо и влево, могут иметь точки покоя, могут иметь седло, в полной совокупности 11 типов интегральных траекторий, которые определяют целостность растительного организма и наступление физиологических событий. Материалы и методы исследования. Прежде, чем строить грубую динамическую систему биологического времени необходимо определить биологическую ось времени. Будем считать, что весь онтогенез разбит на два участка, два отрезка оси биологического времени: Тн≤Т≤Тцв и Тцв≤Т≤Тсозр. Где Тн – начальное значение оси биологического времени, соответствующее биологическому времени, заключенному в семенах растений; Т – текущее значение оси биологического времени; Тцв – точка оси биологического времени соответствующая половине онтогенеза, в наших исследованиях [4,5,6] соответствует моменту цветения; Тсозр – момент завершения онтогенеза, соответствует фазе полного созревания. Тогда ось биологического времени будет описываться дифференциальными уравнениями:
где dT – дифференциал биологической оси времени; dTopt – дифференциал биологической оси времени при оптимальных значениях факторов внешней среды, показывает максимальную скорость развития; dTвнешняясреда – дифференциал биологической оси времени в реальных условиях внешней среды; Usr – уровень напряженности факторов внешней среды, отн. ед., показывает отношение газообмена всего растения при текущих условиях внешней среды к газообмену всего растения при оптимальных условиях внешней среды на данном шаге dT.
где Т – биологическая ось времени, изменяется за весь онтогенез от 0 до 2, отн. ед.; ΔТopt – максимальное приращение биологической оси времени при оптимальных значениях факторов внешней среды, константа, отн. ед.; Usr – уровень напряженности факторов внешней среды за время ΔТ, отн. ед., рассматривается как отношение газообмена всего растения при текущих условиях среды к газообмену растения в оптимальных условиях среды; j – номер шага расчетного периода (номер суток). Для расчетов по уравнениям (3) и (4) используется стандартная гидрометеорологическая информация. Для построения грубой динамической системы биологического времени необходимо проинтегрировать уравнения (1) и (2)
где Здесь мы проинтегрировали уравнение (1), при этом уровень напряженности факторов внешней среды Usr берется не для данного момента онтогенеза, а как некоторое среднее значение от начала момента интегрирования до текущего момента интегрирования. Тогда учтен весь комплекс факторов внешней среды, влияющих на скорость течения биологического времени на определенном отрезке интегрирования. Таким образом, уравнение (5) выражает ось биологического времени в первую половину онтогенеза, на интервале времени Тн≤Т≤Тцв. Поскольку уровень напряженности факторов внешней среды Usr не зависит от биологического времени Т, то эту функцию можно вынести за знак интегрирования
Среднее значение уровня напряженности факторов внешней среды
Подставляя (6) в (5) мы получаем двойной интеграл со своей областью интегрирования
где GF – квадратная область интегрирования со своей границей. Здесь уже рассматривается пространство двух равноправных измерений биологического времени (см. так же [7, 8])
Согласно нашим исследованиям [8] структура биологического времени замкнута, то есть движение времени происходит по замкнутой траектории. Такая постановка вопроса обеспечивается тем, что растение осуществляет постоянный возврат своего организма при каждой вегетации. Развитие начинается с семени и заканчивается опять таки семенем. Поэтому и структура биологического времени должна иметь замкнутый характер движений. В связи с этим, в уравнении (7) мы перейдем к полярным координатам
Область интегрирования GR будет представлять собой круг радиуса ρ;. При этом полярные координаты имеют особую точку ρ=0. Такого значения ρ не может быть, так как в семенах растений всегда находится некоторое не нулевое, структурное образование биологического времени. В то же время, из области GR исключен радиус, лежащий в отрицательных значениях по оси х. В нашем случае ρ; может меняться в пределах
для отрезка биологического времени [ Тн; 1 ]. Учитывая (9), интеграл (8) принимает вид:
где θ; – угол поворота вектора биологического времени. При переходе от уравнения (8) к уравнению (10) мы использовали следующую конструкцию: мы рассматриваем движения биологического времени в координатной плоскости переменных TF и TR; при этом считается, что физическое время имеет свойство движения равномерно слева направо; движения биологического времени осуществляются по кругу; точнее от -π; до +π; не совершая полного оборота; в этом случае взаимосвязь физического и биологического времен, как переход от (8) к (10) осуществится как интегрирование уравнения (10). Теперь мы можем перейти непосредственно к грубой динамической системе биологического времени. Рассмотрим подынтегральное выражение уравнения (10). Это дифференциальное уравнение двух переменных. Оно имеет вид определителя
и, согласно работам Л.С. Понтрягина и А.А Андронова [9], являются вторыми производными дифференциальной системы уравнений:
Нам остается найти явный вид системы дифференциальных уравнений (А). Для этого необходимо проинтегрировать один раз систему дифференциальных уравнений в частных производных (11):
Таким образом, мы нашли автономную систему двух дифференциальных уравнений в пространстве двух переменных: Т и θ;. Здесь, в (12) переменная t является физическим временем, которое течет равномерно и прямолинейно. Будем считать систему (12) полной для двухмерного случая. Система (12) определяет структуру биологического временного поля для первой половины онтогенеза. Для второй половины онтогенеза аналогично получим:
Таким образом, мы получили две системы двух дифференциальных уравнений: (12) и (13) для двух отрезков онтогенеза до цветения и после цветения. Переход от одной системы уравнений (12) к другой системе уравнений (13) осуществляется в растении в момент цветения. Ниже мы построим фазовый портрет системы (12) следующим методом, изложенным в [10]. Для изображения фазового портрета необходимо построить векторное поле направлений траекторий системы (А) в каждой точке фазовой плоскости. Задавая приращение Δt>0, получим соответствующие приращения Δх и Δу из выражений:
Тогда направление вектора Результаты исследования и их анализ. Теоретические результаты. Будем считать выполненными условия теорем существования грубой динамической системы биологического временного поля растений (12) [9]. Тогда мы получаем следующие теоретические результаты. В полной совокупности грубая динамическая система биологического временного поля растений дает 11 типов интегральных траекторий времени [9], табл. 1. Эта таблица получена на основе сопоставления результатов [9] и результатов цитологических исследований, изложенных в [11]. Основные типы интегральных траекторий автономной динамической системы (А) представлены на рис. 1.
Таблица 1 - Совокупность интегральных траекторий системы биологического временного поля растений (12) в сопоставлении с клеточной структурой растений
Рисунок 1 – Основные типы интегральных траекторий автономной динамической системы биологического временного поля. λ1, λ2 – корни характеристического уравнения грубой динамической системы биологического временного поля (по данным [10]).
Кроме того, мы можем отметить, что динамическая система (12), а так же (13) разбивает область GR на конечное число связных ячеек – растительных клеток, заполненных обыкновенными временными траекториями. Такие клетки разбиваются на два класса: на класс клеток, примыкающих к циклу без контакта, и на класс внутренних клеток. Каждая такая клетка имеет в составе границы одну особую траекторию, являющуюся «элементом притяжения», или стоком, и одну особую траекторию, являющуюся «элементом отталкивания», или, источником. Каждая клетка имеет в составе границы одну особую траекторию, являющуюся стоком [9]. Будем считать, что для систем (12) и (13) существует взаимно однозначное и взаимно непрерывное преобразование области GR в себя. Тогда качественная структура разбиения этих временных областей на траектории определяется особыми траекториями, направлением движения по замкнутым траекториям и характером устойчивости предельных особых траекторий [9]. Это утверждение означает, что предельный цикл, отвечающий клеточному ядру, определяет управляющую структуру растительного организма. В то же время существуют и другие траектории, отвечающие другим растительным структурам (другим структурам клетки). К теоретическим результатам можно отнести так же и следующее. Временная структура по типу седла сопоставляется с хроматином клетки. Тогда, на основании [9], сепаратрисы (усы седла) в нормальном состоянии клетки не идут из седла в седло. Это означает, что клетка не делится и хроматин находится в свободном состоянии. Как только (с движением биологического времени) усы седла начинают идти из седла в седло происходит разрыв грубости системы - движение хроматина (образуется веретено), клетка делится. Результаты исследования и их анализ. Практические результаты. Фазовый портрет системы дифференциальных уравнений (12) для двух переменных Т и θ; представлен на рис. 2. Область GR заключена в пределах: 0,01≤Т≤1 и 0,01≤θ+π; и соответствует целостности растительного организма. Для определенности мы будем считать, что этот фазовый портрет соответствует культуре подсолнечника. Шаг разрешения Δt составляет значение 1/5000, что соответствует 15 минутам физического времени. Это время может меняться в зависимости от состояния факторов внешней среды. Константы интегрирования с1 и с2 составляют соответственно значения: с1=0.65 отн. ед. биологического времени и с2=0.28 отн. ед. биологического времени. Уровень напряженности факторов внешней среды Usr является постоянным, хотя на протяжении вегетационного периода происходит его изменение в зависимости от состояния агрометеорологических факторов. Напомним, что уровень напряженности факторов внешней среды Usr определяется как отношение скорости газообмена всего растения в текущих условиях среды к скорости газообмена всего растения в оптимальных условиях среды. Для нашего случая Usr=0.8 отн. ед. Видно, что в целом область существования переменных Т и θ; разбита особой траекторией на две области: верхняя и нижняя. При этом граница разбиения является прямой линией. Верхняя часть области GR соответствует надземной части растений, а нижняя – корням. В целом видно, что корни интенсивно растут в начале вегетационного периода (мы рассматриваем период от посева до цветения), и граница области имеет вид параболы. Надземная часть растения растет равномерно, в соответствии с изменениями биологического временного поля. В верхней, надземной части области GR видны траектории по типу седла. Их несколько, конечное число. При чем нулевые точки расположены по прямой линии. Эти траектории можно отождествить с функцией конуса нарастания - сначала закладываются листья и потом репродуктивные органы (корзинка) подсолнечника Видно, что траектории по типу седла расположены в начале исследуемого периода времени, что соответствует интенсивному заложению органов в конусе нарастания растений, заложение примордиев. Таким образом, мы можем вычислить время пластохрона как последовательность нулевых точек по типу седла. Отметим так же и то, что траектории по типу седла имеют сепаратрисы идущие из седла в седло. Это означает, что на этих траекториях нарушаются условия грубости системы биологического времени и система стает негрубой: происходит интенсивное деление меристематической ткани, закладываются новые органы. Можно так же отметить следующее. Верхняя и нижняя части области GR различны. В верхней части области, соответствующей надземной части растений присутствует траектории по типу седла. В нижней части области GR соответствующей корням таких траекторий не
dt = Δt =1/5000 – шаг разрешения (15 мин), весь период времени от 0 до 5000 соответствует периоду времени 0.01≤Т≤1 или Тн≤Т≤Тцв (53-е суток); О=θ; – угол поворота вектора времени.
Рисунок 2 – Фазовый портрет грубой динамической системы биологического времени растений (12) (для подсолнечника). видно. Заметно лишь, что в нижней части этой области происходит интенсивное деление клеток, что соответствует росту корней в своих точках роста. В целом, область GR разбита на конечное число связных ячеек – клеток, как показано в работе Л.С Понтрягина и А.А Андронова [9]. Отметим так же и то, что мы получили временную структуру, которая отвечает жизненным проявлениям организма растения. Заключение. Таким образом, получена временная структура, которая определяет целостность организма растения с подразделением этого организма на составляющие его растительные клетки. Временная структура рассматривается в двухмерном измерении – временной плоскости. При этом, траектории биологического временного поля пронизывают весь организм растения. На различных видах траекторий проходят свои физиологические процессы. Тем самым, такая временная структура определяет биохимические процессы в растении и в каждой клетке, их направленность. Хочется выразить признательность за доброжелательную критику моих исследований профессору А.Н. Полевому.
Список литературы
|


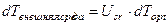 , Тн≤Т≤Тцв, (1)
, Тн≤Т≤Тцв, (1) , Тцв≤Т≤Тсозр, (2)
, Тцв≤Т≤Тсозр, (2)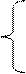 Разностная форма расчетов имеет вид:
Разностная форма расчетов имеет вид: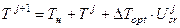 , Тн≤Т≤Тцв, (3)
, Тн≤Т≤Тцв, (3) , Тцв≤Т≤Тсозр, (4)
, Тцв≤Т≤Тсозр, (4) , Тн≤Т≤Тцв, (5)
, Тн≤Т≤Тцв, (5)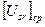 - среднее значение напряженности факторов внешней среды от момента времени Тн до текущего значения Т.
- среднее значение напряженности факторов внешней среды от момента времени Тн до текущего значения Т.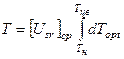 .
. . (6)
. (6)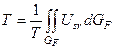 , (7)
, (7)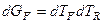 .
.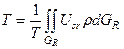 . (8)
. (8)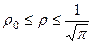 , (9)
, (9)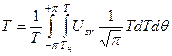 , (10)
, (10)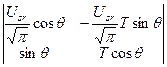 (11)
(11) ;
; 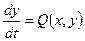 . (А)
. (А)
 .
. (12)
(12)

 (13)
(13) , (В1)
, (В1) . (В2)
. (В2) в точке (х,у) определит структурную организацию поля без явного, аналитического решения системы уравнений (А). Построение фазового портрета позволяет сделать выводы о характере изменений переменных х, у без знания аналитических решений исходной системы уравнений (А).
в точке (х,у) определит структурную организацию поля без явного, аналитического решения системы уравнений (А). Построение фазового портрета позволяет сделать выводы о характере изменений переменных х, у без знания аналитических решений исходной системы уравнений (А).




