Работа 1. Уравнение Ван-дер-Ваальса
ИЗУЧЕНИЕ СВОЙСТВ РЕАЛЬНЫХ ГАЗОВ (Уравнение Ван-дер-Ваальса, эффект Джоуля – Томсона)
Цель работы
1. Изучение свойств реальных газов и анализ их отличий от идеальных газов на примере атмосферного воздуха. 2. Определение константы а, входящей в уравнение Ван-дер-Ваальса для атмосферного воздуха (работа 1). 3. Изучение процесса дросселирования и экспериментальное определение коэффициента дросселирования (эффект Джоуля–Томсона) для атмосферного воздуха (работа 2).
Основные теоретические положения
Работа 1. Уравнение Ван-дер-Ваальса Отличия свойств реальных газов от идеальных обусловлены наличием сил межмолекулярного взаимодействия и размерами самих молекул, которые в модели идеального газа не учитываются [1, 2, 3]. Уравнение состояния идеального газа Менделеева–Клапейрона (2.1) применять для реальных газов можно только при малых давлениях, когда расстояния между молекулами несоизмеримо велики по сравнению с размерами самих молекул, а силы межмолекулярного взаимодействия практически отсутствуют.
где p – абсолютное давление газа, Па; v – удельный объем газа, м3/кг; R – газовая постоянная, Дж/(кг К); Т – абсолютная температура, К. Первую попытку получить уравнения реального газа сделал голландский ученый Я. Ван-дер-Ваальс в 1887 году. Он предложил усовершенствовать уравнение Менделеева–Клапейрона и применять его в виде
где а – константа, учитывающая силы межмолекулярного взаимодействия данного газа; b – константа, учитывающая объем, занимаемый самими молекулами данного газа. Константы a и b в уравнении (2.2) для каждого газа имеют свои значения и могут быть определены экспериментально. Однако это уравнение не является универсальным и имеет узкую, ограниченную для каждого газа своими параметрами Р и Т область применения. Но данное уравнение имеет важное значение при изучении свойств реальных газов, поскольку при его записи в безразмерном виде (все входящие в него параметры делятся на соответствующие параметры в критической точке) получается уравнение справедливое для любого газа:
где p=p/pкр – приведенное критическое давление; w=Т/Ткр – приведенная критическая температура; t=v/vкр – приведенный критический объем. Уравнение (2.3) не содержит ни одной константы, определяемой свойствами конкретного газа, следовательно, оно применимо к любому газу, подчиняющемуся уравнению Ван-дер-Ваальса. Кроме этого, если различные газы имеют одинаковые приведенные параметры p, w, t, они будут термодинамически подобными и для нахождения констант уравнения (2.2) достаточно знать только критические параметры данного газа, а сами константы можно рассчитать по формулам
Формулы (2.4) – (2.6) получены из уравнения (2.2) путем приравнивания первой и второй производной к нулю при Т=const для критической точки [2,4]. Параметры состояния вещества в критической точке характеризуют в общем виде силы молекулярного взаимодействия данного вещества. Принадлежность газа к ван-дер-ваальсовому газу можно оценить соотношением
У ван-дер-ваальсовых газов Zкр=0,375 [1]. В данной работе изучаются свойства реального газа в виде атмосферного воздуха. Для сухого воздуха (m=28,96 кг/кмоль) параметры критической точки соответствуют значениям [4] ркр=3,72 МПа, tкр=140 оС, vкр=3,226х10-3 м3/кг. Из соотношения (2.7) получим величину Zкр:
Следовательно, атмосферный воздух близок по свойствам к ван-дер-ваальсовому газу. Применив соотношения (2.4), (2.5), определим расчетным путем константы a и b для воздуха в уравнении (2.2):
Коэффициент а можно получить и из соотношения (2.6):
Разница в числовых значениях коэффициента а, полученного из соотношений (2.5) и (2.6), говорит о том, что уравнение Ван-дер-Ваальса не универсально и дает определенную погрешность в расчете параметров реальных газов при его использовании. Однако для параметров атмосферного воздуха оно применимо. В этом мы убедимся в ходе выполнения лабораторной работы при определении опытным путем коэффициента а. Если коэффициент а будет находиться в диапазоне значений 0 ¸ 139, Коэффициент а можно определить из уравнения (2.2), подставив в него параметры газа, определенные экспериментально для какого - то состояния газа. При опытном определении термических параметров в двух состояниях газа можно определить оба коэффициента – а и b, решив систему двух уравнений (2.2) с двумя неизвестными. В данной лабораторной работе осуществляется процесс адиабатного дросселирования воздуха с фиксацией параметров воздуха до и после дросселирования. Эти параметры позволяют определить коэффициент а как вышеуказанным методом, так и с помощью уравнения процесса дросселирования h2=h1, (2.8) которое можно записать через внутреннюю энергию как u2+p2v2 = u1+p1v1 . (2.9) Особенностью внутренней энергии ван-дер-ваальсовского газа является то, что она является функцией и температуры, и объема, о чем свидетельствует выражение, полученное в [4] на основании уравнения (2.2):
При этом теплоемкость сv этого газа зависит только от температуры. Исходя из этого, внутреннюю энергию ван-дер-ваальсового газа можно представить выражением
условно считая изохорную теплоемкость величиной постоянной. Используя уравнение (2.11), выражение (2.9) можно представить в виде
Процесс дросселирования воздуха идет с малым изменением температуры, поэтому изохорные теплоемкости в начале и конце процесса можно считать одинаковыми (cv1=cv2). Используя эти допущения, выразим из уравнения (2.12) константу а:
В лабораторной работе для определения константы а можно использовать оба метода, т.е. можно использовать уравнения (2.2) и (2.13).
2.2. Работа 2. Эффект Джоуля – Томсона
Изменение температуры реальных газов в процессе адиабатного дросселирования обусловлено отличием их свойств от свойств идеальных газов. Это явление впервые было объяснено учеными Джоулем и Томсоном (лорд Кельвин) в 1852 г. [2]. Они ввели коэффициент ah, характеризующий изменение температуры в процессе дросселирования:
Это – коэффициент адиабатного дросселирования, или дифференциальный дроссель-эффект Джоуля – Томсона. Поскольку в процессе дросселирования dр<0, то при ah>0 температура будет уменьшаться, а при ah<0 – увеличиваться. Объяснить изменение температуры реального газа при дросселировании можно, проанализировав изменение кинетической составляющей внутренней энергии в этом процессе. В соответствии с уравнениями (2.8) и (2.9) изменение внутренней энергии в процессе дросселирования определяется выражением u2 - u1 = p1v1 - p2v2 = Duк + Duп, (2.15) где Duк и Duп – изменение кинетической и потенциальной составляющих внутренней энергии. Следовательно, кинетическую составляющую изменения внутренней энергии можно представить уравнением Duк = (p1v1 - p2v2) - Duп. (2.16) Потенциальная составляющая изменения внутренней энергии в процессе дросселирования газа всегда возрастает (Duп>0), т.к. объем газа увеличивается. Следовательно, изменение кинетической составляющей внутренней энергии определяется знаком и величиной первого слагаемого правой части выражения (2.16). При этом возможны следующие варианты: 1) -(p2v2 - p1v1) - Duп = 0, Duк = 0, dT = 0; 2) -(p2v2 - p1v1) - Duп < 0, Duк <0, dT < 0; 3) -(p2v2 - p1v1) - Duп > 0, Duк > 0, dT > 0. В свою очередь, значение (p2v2 - p1v1) характеризует отличие свойств идеальных газов от свойств реальных газов, т.к. это не что иное, как характеристика Для реальных газов в процессе дросселирования температура обычно уменьшается или остается неизменной. Для жидкой фазы веществ возможны все варианты поведения температуры в процессе дросселирования. Исходя из вышеизложенного это объясняется областью параметров р и t, где происходит процесс дросселирования конкретного вещества.
|

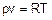 , (2.1)
, (2.1) , (2.2)
, (2.2) , (2.3)
, (2.3) , (2.4)
, (2.4)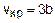 , (2.5)
, (2.5)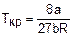 . (2.6)
. (2.6)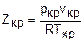 . (2.7)
. (2.7) .
. м3/кг;
м3/кг;
 .
.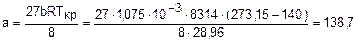 .
.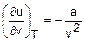 . (2.10)
. (2.10)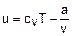 , (2.11)
, (2.11)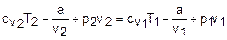 . (2.12)
. (2.12) . (2.13)
. (2.13) . (2.14)
. (2.14) , указывающая на отличие сжимаемости
, указывающая на отличие сжимаемости  в процессе дросселирования реального газа от сжимаемости идеального [3]. Она указывает на то, что при
в процессе дросселирования реального газа от сжимаемости идеального [3]. Она указывает на то, что при 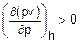 сжимаемость реального газа меньше сжимаемости идеального и для реального газа в процессе дросселирования температура будет уменьшаться (см. вариант 2), при
сжимаемость реального газа меньше сжимаемости идеального и для реального газа в процессе дросселирования температура будет уменьшаться (см. вариант 2), при  сжимаемость реального газа больше сжимаемости идеального и для реального газа в процессе дросселирования температура может уменьшаться, оставаться неизменной или увеличиваться в зависимости от значения модуля величины (p2v2 - p1v1) (см. вариант 3).
сжимаемость реального газа больше сжимаемости идеального и для реального газа в процессе дросселирования температура может уменьшаться, оставаться неизменной или увеличиваться в зависимости от значения модуля величины (p2v2 - p1v1) (см. вариант 3).


