Лабораторной работы 1
В соответствии с разд. 3 проводится опыт и заполняется журнал наблюдений.
Журнал наблюдений к работе 1
Дата «__»______200 г. Подпись студента ________________ Подпись преподавателя ___________ Атмосферное давление В=__ мм рт. ст. Показания термометра в лаборатории tо=__ oC
Таблица 4.1. Экспериментальные данные
В табл. 4.1 приведены следующие величины: tо1 и tо2 – температуры воздуха до и после дроссельного устройства в начале опыта; t1оп и t2оп – температуры воздуха до и после дроссельного устройства в конце опыта; Dр – перепад давлений на дроссельном усройстве; N – число делений на шкале ротаметра, соответствующее положению его поплавка во время опыта. Первоначально определяется объемный расход воздуха через установку. Для этого необходимо перевести показания ротаметра в объемный расход воздуха при параметрах воздуха в опыте (по табл. 4.2). Таблица 4.2. Градуировочная шкала ротаметра
Аппроксимированное выражение массового расхода по ротаметру соответствует уравнению
где G – массовый расход воздуха, кг/с; N – число делений на шкале ротаметра. Перерасчет объемного расхода воздуха градуировочной шкалы ротаметра на действительные параметры воздуха выполняется по формуле
где
ρо – плотность воздуха по градуировочной таблице ротаметра, ρо=1,18 кг/м3; ρ2 – плотность воздуха при его параметрах на входе в ротаметр, кг/м3. Плотность воздуха на входе в ротаметр определяется по уравнению состояния идеального газа
где р2 – давление воздуха на входе в ротаметр, принимается равным атмосферному давлению; Т2 – температура воздуха на входе в ротаметр. Абсолютные значения температур перед дроссельным устройством t1 и за ним t2 корректируются по значениям температур в начале и конце каждого опыта в соответствии с выражением
где Массовый расход воздуха G, кг/с, проходящего через установку, не требует корректировки значения в зависимости от параметров воздуха на входе в ротаметр. Значение удельного объема на входе в ротаметр определяется уравнением
Значение удельного объема перед дроссельным устройством определяется по уравнениям состояния идеального газа до и после дросселирования в соответствии с выражениями
где р1 и р2 – давления воздуха до и после дросселирования. Давления р1 и р2 рассчитываются по уравнениям
Полученные величины записывают в табл. 4.3 результатов обработки опытных данных. Таблица 4.3. Результаты обработки опытных данных
Далее определяется константа уравнения Ван-дер-Ваальса а для воздуха. Расчет этой константы в данном опыте возможен двумя методами.
Метод 1. Определение константы а непосредственно из уравнения Ван-дер-Ваальса
Этот метод базируется на уравнении (2.2), когда константа b принимается равной нулю. Такое допущение не внесет большой погрешности в определении константы а, т.к. при данных параметрах воздуха собственный объем молекул воздуха несоизмеримо мал с объемом, занимаемым воздухом. Расчетное выражение этой константы в данном случае будет иметь вид
где параметры воздуха соответствуют состоянию воздуха за дроссельным устройством.
Метод 2. Определение константы а по процессу дросселирования воздуха
В этом методе используется уравнение (2.13)
в котором сv – удельная массовая изохорная теплоемкость воздуха, величина постоянная, рассчитывается по уравнению идеального газа. Результаты в определении константы а по этим методам могут иметь расхождение. Необходимо сделать вывод, какой из этих методов дает более точный результат, сопоставив опытные значения констант а со значениями этой константы, приведенными в разд. 2.1.
|

 ×106, м3/с
×106, м3/с
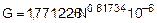 , (4.1)
, (4.1) , (4.2)
, (4.2)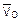 – объемный расход воздуха по градуировочной таблице ротаметра, м3/с;
– объемный расход воздуха по градуировочной таблице ротаметра, м3/с;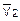 – объемный расход воздуха в пересчете на параметры воздуха перед ротаметром в опыте, м3/с;
– объемный расход воздуха в пересчете на параметры воздуха перед ротаметром в опыте, м3/с; , (4.3)
, (4.3) , (4.4)
, (4.4) и
и 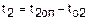 .
. . (4.5)
. (4.5)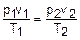 ,
, 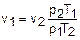 , (4.6)
, (4.6)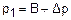 ,
,  . (4.7)
. (4.7)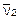
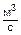
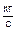


 , (4.8)
, (4.8) ,
,


