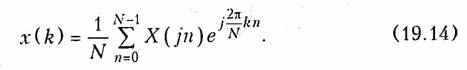Спектр дискретного сигнала
Преобразование Фурье для дискретного сигнала. Определим связь между спектром X(jω) аналогового сигнала х(t) и спектром Xт(jω) дискретного сигнала xT(t), определенного моделью (19.2). Учитывая, что хT(t) = x(t)f(t) согласно теоремы свертки (9.30) получим спектральную плотность дискретного сигнала
Подставив (19.6) в формулу (19.4) после изменения порядка интегрирования и суммирования и с учетом фильтрующего свойства δ-функцни окончательно получим
Из (19.7) следует важный вывод: спектр дискретного сигнала xT(t) (рис. 19.6 б) представляет собой сумму бесконечно большого числа «копий» спектра аналогового сигнала (рис. 19.6, а), расположенных, на оси частот через одинаковые интервалы. Следует отметь, что согласно (19.7) и рис. 19.6, б энергия спектра дискретного сигнала оказывается бесконечно велика, что является следствием идеализации реального сигнала моделью (19.2).
Если же использовать вместо дискретнзирующей последовательности (19.1) последовательность импульсов конечной энергии (например, прямоугольных импульсов), то получим спектр xT(jω), энергия которого убывает с ростом ω («копни» X(jω) с ростом ω уменьшаются). В то же время следует еще раз подчеркнуть, что представление дискретного сигнала в форме (19.2) существенно упрощает анализ дискретных сигналов и цепей и широко используется в расчетах. Спектр дискретного сигнала ХT(jω) можно найти и непосредственно из прямого преобразования Фурье (9.6) для дискретного сигнала (действует в момент t ≥ 0).
На практике в формулах (19.8), (19.9) часто вместо зависимости ХT(jω) рассматривают зависимости XT(jf), которые легко можно получить путем замены ω = 2πf. Следует отметить, что если не выполняется условие теоремы Котельникова: fД ≥ 2fB, то спектры в (19.7) частично перекрываются. На рис. 19.9, рис. 19.10 показан характер изменения спектра дискретного сигнала ХT(f) при изменении частоты дискретизации сигнала xT(t), ограниченного во времени интервалом Тс (рис. 19.9) н неограниченного во времени (рис. 19.10). Как следует из представленных графиков увеличение периода дискретизации Т >1/2FB; FД < 2FB приводит к наложению смежных спектров в (19.7), что приводит к наложению спектра ХT(f). Эти искажения называются ошибками наложения. Чтобы их устранить необходимо частоту дискретизации увеличить до FД ≥ 2FB. Пример. Рассчитаем интервал дискретизации и минимально допустимую частоту дискретизации сигнала, спектральная плотность которого равна нулю при значениях частоты выше 100 кГц. Из условия задачи следует, что граничная частота спектра FВ равна 100 кГц. Тогда и соответствии с теоремой Котельникова имеем интервал дискретизации
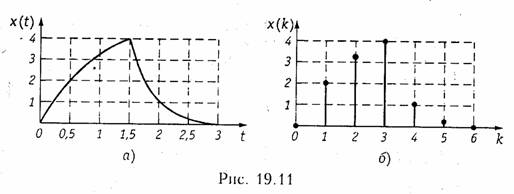
Минимально допустимая частота дискретизации f д = 2Fb = 2-100 = 200 кГц. Пример. Определим дискретные отсчеты сигнала длительностью t и = 3 мс, приведенного на рис. 19.11, а, если в качестве граничной частоты спектра FВ принять значение З/tи, выше которого все значения спектральной плотности уменьшаются более чем в 10 раз по сравнению с максимальным. Хотя сигнал конечной длительности имеет бесконечный спектр частот, однако почти всегда можно определить граничную частоту спектра таким образом, чтобы отсекание частот превышающих FВ, привело к пренебрежимо малым изменениям энергии исходного сигнала. Такое условие задано в примере.
Отметим, что аналоговый сигнал x(t) можно полностью восстановить по его дискретным отсчетам x(kT) с помощью ФНЧ, частота среза которого
а из которого видно, что спектр сигнала на выходе ФНЧ совпадает со спектром аналогового сигнала x(t). Дискретное преобразования Фурье. Как следует из формулы (19.7) ХT(jω) имеет периодическую структуру с ωд = 2π/Т. Причем, как и спектр аналогового сигнала X(jω) спектр дискретного сигнала ХT(jω) является сплошным (см. рис. 19.6, 6). Вместе с тем при цифровой обработке сигналов используется не только дискретизация во времени, но и дискретизация в частотной области. Для сигнала x(t) ограниченного во времени интервалом Тс (рис. 19.12, а) справедлива обратная теорема Котельникова, которая может быть получена из (19.3) путем замены
С учетом вышеизложенного дискретное преобразование Фурье (ДПФ) можно получить, если в преобразовании (19.8) сделать замену ω= nΔω. Тогда получим
которое определяет прямое ДПФ. С помощью (19.13) можно определить отсчеты спектра X(jn) по временным отсчетам сигнала x(k). Обратное ДПФ можно получить из (19.13) воспользовавшись дуальностью прямого и обратного преобразований Фурье:
При k < О обратное преобразование Фурье определит x(k), расположенную слева от 0 (рис. 19.12, в). Для ДПФ по аналогии с непрерывными преобразованиями Фурье справедливы основные теоремы и свойства (см. § 9.2). В частности, свойство линейности
т. е. сдвиг последовательности отсчетов сигнала на т интервалов приводит лишь к изменению фазового спектра дискретного сигнала. Теорема свертки:
Аналогично можно записать н другие теоремы для ДПФ. Заметим, что ДПФ можно использовать для определения не только спектра дискретных сигналов, но и спектра аналоговых сигналов, для чего его необходимо дискретизировать согласно теоремы Котельникова (19.3). Для сокращения вычислений используют обычно алгоритм быстрого преобразования Фурье (БПФ). Существует много разновидностей БПФ.
|







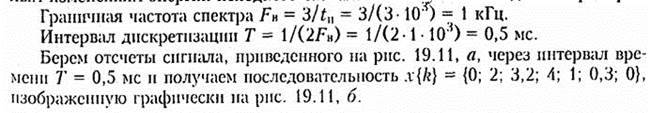
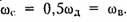 Этот вывод хорошо иллюстрирует рис. 19.10,
Этот вывод хорошо иллюстрирует рис. 19.10,