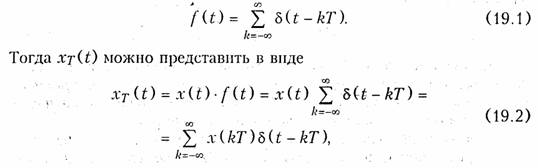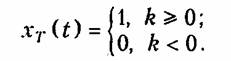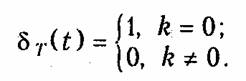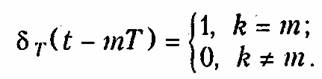Дискретные сигналы

Л 19-20. Методы анализа дискретных цепей

 

Дискретные сигналы

 

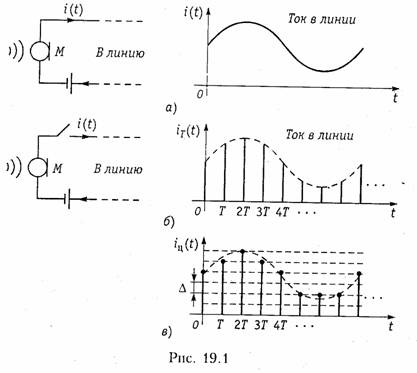
Дискретизация аналоговых сигналов. Сигнал — это физический процесс (например, изменяющиеся во времени токи и напряже­ния), содержащий в себе некоторую информацию. Любой сигнал можно описать математической функцией.

Существуют аналоговые, дискретные и цифровые сигналы. Аналоговые сигналы описываются непрерывной во времени функ­цией x(t), которая может принимать любые значения в определен­ном интервале (рис. 19.1, а); дискретные сигналы x_Т(t) представ ля ют собой последовательности или отсчеты функции x(t), взятые в определенные дискретные моменты времени kT (рис. 19.1, б); цифровыми являются сигналы, которые в дискретные моменты времени kT принимают конечные дискретные значения — уровни квантования (рис. 19.1, в), которые затем кодируются двоичными числами. (На рис. 19.1, в, Δ — шаг квантования).

Если в цепь микрофона (рис. 19.1), где ток i(t) является не­прерывной функцией времени, встроить ключ и периодически на короткие мгновения замыкать его, то ток в цепи будет иметь вид узких импульсов с амплитудами, повторяющими форму непрерыв­ного сигнала. Последовательность этих импульсов, которые назы­вают отсчетами непрерывного сигнала, и представляет собой, не

что иное, как дискретный сигнал. Причем, во всех этих записях k — целое число, принимающее как положительные, так и отрица­тельные значения.

В отличие от непрерывного сигнала i(t) дискретный сигнал можно обозначить i_Т(t). Так, на рис. 19.1 при k < О дискретный сигнал i_Т(t) = 0. При k = 0 значение i_Т(ОТ) равно значению сиг­нала i(t) в момент времени t = 0. При k > 0 отсчеты i(kT) повто­ряют форму сигнала i(t), т. к. их амплитуды равны значениям непрерывного сигнала в моменты времени kT.

Дискретные сигналы можно задавать графиками, как это пока­зано на рис. 19.1, формулами, например, i_T(t) = sin(2πfkT), в виде таблиц дискретных значений или другими способами.

Математическая модель дискретного сигнала. Аналитически дискретный сигнал x_Т(t) удобно представлять с помощью дискретизирующей последовательности δ; -функций:

т. е. дискретный сигнал х_Т(t) с помощью (19.2) представляется в виде последовательности δ-функций с весовыми коэффициентами, равными отсчетам x(kT) аналогового сигнала x(t) в точках kT. На рис. 19.2 изображена схема, иллюстрирующая процедуру форми­рования дискретного сигнала согласно формулы (19.2).

Рассмотрим примеры некоторых дискретных сигналов, полу­ченных из типовых аналоговых сигналов.

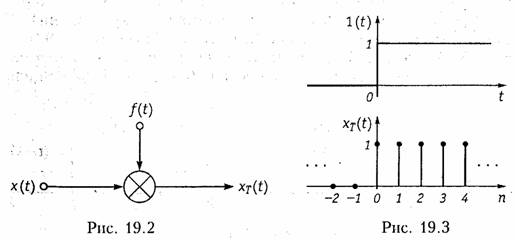
Пример. Единичный ступенчатый аналоговый сигнал 1(t) приведен на рис. 19.3.

Соответствующий ему дискретный сигнал x _Т (t) называется ступенчатой последовательностью. Он определяется следующим образом:

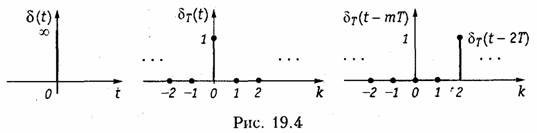
Такая последовательность приведена на рис. 19.3.

Пример. Импульс Дирака или δ-функция в аналоговой области приведена на рис. 19.4.

Дельта-последовательность или дискретная δ -функция определяется выра­жением

Последовательность δ_т(t), приведенная на рис. 19.4, принимает единст­венное значение, равное 1, при k= 0. Этот сигнал можно сдвинуть на т ин­тервалов (рис. 19.4):

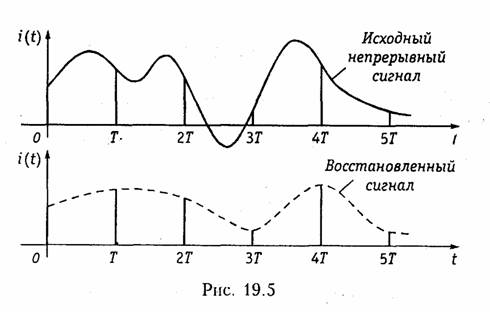
Интервал времени Т, через который отсчитываются значения непрерывного сигнала i(t), называется интервалом дискретиза­ции. Обратная величина 1/Т (обозначим ее f_д) называется часто­той взятия отсчетов или частотой дискретизации.

Отсчеты непрерывного сигнала следует брать с такой частотой (или через такой интервал времени), чтобы успевать отследить все, даже самые быстрые, изменения сигнала. Иначе, при восстановлении этого сигнала по дискретным отсчетам часть информации будет поте­ряна и форма восстановленного сигнала будет отличаться от формы исходного (рис. 19.5). Если обратиться к схеме рис. 19.1, то это оз­начает, что звук на приеме будет восприниматься с искажениями.

Для сигналов с ограниченным спектром, т. е. сигналов, у кото­рых спектр ограничен некоторой верхней частотой ω_в = 2πF_B суще­ствует теорема Котельникова, определяющая выбор интервала дискретизации Т (или, что то же, частоты дискретизации). Эта теорема впервые была доказана В.А. Котельниковым в 1933 г. в работе «О пропускной способности «эфира» и проволоки в элек­тросвязи» ставшей основополагающей в теории и технике цифро­вой связи.

Теорема Котельникова. Если функция х(t) имеет спектр, ог­раниченный верхней частотой F_B, то x(t) полностью определя­ется последовательностью своих значений {.отсчетов) в момен­ты времени, отстоящие друг от друга на период Т ≤1/2F_B.

Математически теорема Котельникова записывается следующим образом

Доказательство теоремы Котельникова дается в общей теории свя­зи. Здесь же отметим, что функция вида sinω_Bt'/ω_Bt' (t’ = t — kT) известна нам как функция отсчетов (см. § 5.3), поэтому теорему Котельннкова иногда называют еще теоремой отсчетов.

Физический смысл теоремы Котельникова (19.3) заключается в том, что непрерывная функция x(t) с ограниченным спектром F_B полностью может быть восстановлена, если известны ее отсчеты, взятые через интервал Т ≤ 1/2F_B. Эта теорема играет очень большую роль в теории связи, т. к. позволяет передачу аналого­вых сигналов заменить передачей дискретных или цифровых сигналов, что позволяет существенно повысить эффективность систем связи.