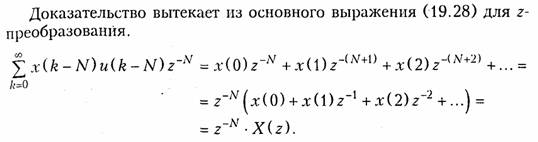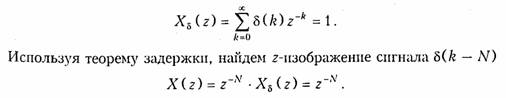Z-преобразование и его свойства

 

При анализе и синтезе дискретных и цифровых цепей широко применяют так называемое z-преобразование. Это преобразование играет такую же основополагающую роль по отношению к дис­кретным сигналам, как преобразование Лапласа по отношению к аналоговым сигналам.

Z-преобразование дискретного сигнала. Заменим в уравнении (19.8) jω на комплексную переменную р:

 

где интегрирование осуществляется по окружности с радиусом │z│=1

Доказать справедливость (19.29) можно следующим образом. Пусть X(z) — функция комплексной переменной z, аналитическая в области |z| > r_о. Рас кроем ряд (19.28):

Установим связь между точками на комплексной плоскости р = α+ j ω и z-плоскости z= х + jу (рис. 19.16).

Если положить α = 0, то мы будем перемещаться по оси j ω в плоскости р. При переходе в z-плоскость точки мнимой оси j ω бу­дут располагаться на единичной окружности z = е ^{j ω T}. Причем, точка j0 на р - плоскости переходит в точку z = +1 на вещественной оси 2-плоскостн, а точки ±j0,5 ω _д — в точку z = — 1. Это означает, что точки отрезка (-j0,5 ω _д ÷j0,5 ω _д) р - плоскости проектируются в точки на единичной окружности z-плоскости. Так как функция z = е^{± j ω T}периодическая, то последующие отрезки оси j ω на р -плоскости такой же длины будут вновь проектироваться на единичную окружность.

Точкам левой р - полуплоскости соответствуют точки внутри еди­ничной окружности z-плоскости, а точкам правой р - полуплос­кости — точки вне этой окружности.

Свойства z -преобразования. Так же как и для преобразований Лапласа и Фурье, существуют теоремы для z -преобразования. Приведем наиболее важные теоремы одностороннего z-преобразования.

Теорема линейности (суперпозиции). Сумме дискретных сиг­налов соответствует сумма их z-изображений. Если дискретным сигналам x(k) и y(k) соответствуют г-изображения Х(z) и Y(z), то

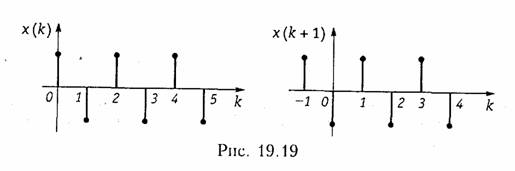
где а и Ь — некоторые числа.

Доказательство теоремы выполните самостоятельно, используя выражение (19.28) для расчета z-изображения дискретного сигнала.

Теорема опережающего сдвига. Если дискретному сигналу x(k) соответствует одностороннее z -преобразование X(z), то сигналу, вдвинутому на один интервал дискретизации, x(k + 1) соответст­вует z -преобразование z(X(z) — х(0)).

 

 

 

 

При доказательстве учтено, что единичная ступенчатая функция обращается в нуль при отрицательных значениях ее аргумента, т. е. при п < N. Из теоремы задержки в частности следует, что сдвиг дискретного сигнала на один интервал дискретизации Т со­ответствует умножению z -преобразования на оператор z^-1, поэтому часто z^-1 называют оператором единичной задержки в z -области.

Теорема умножения на а^k. Математическая запись теоремы имеет вид

Эту теорему мы приводим здесь без доказательства. При необ­ходимости с ним можно познакомиться в специальной литературе.

Пример. Найдем z - преобразование функции единичного отсчета, задер­жанной на N интервалов дискретизации.

Найдем z -преобразование дискретного δ-импульса δ(k) (рис. 19.4), исполь­зуя выражение (19.28)

 

На рисунке 19.4 приведен также график задержанной функции единично­го отсчета для частного случая N = 2.

 

 

 

В табл. 19.1 дана сводка z- преобразованной наиболее часто встречающихся дискретных последовательностей. Эти табличные сведения также могут быть использованы для расчета z -преобразований сигналов и перехода от z-преобразований к дискретным сиг­налам.

Пример. Найдем общий член дискретного сигнала x(k), которому соответ­ствует z -изображение