НА ОСНОВЕ ЭКСПЕРТНЫХ ЗНАНИЙ

Лабораторная работа № 2

по дисциплине:

Прикладные нечёткие системы

на тему:

РАЗРАБОТКА НЕЧЁТКОЙ СИСТЕМЫ ТИПА СУГЕНО

НА ОСНОВЕ ЭКСПЕРТНЫХ ЗНАНИЙ

 

Выполнил:

студент группы ВТМ-11

Соколов И.П.

Проверил:

доцент Боцула Л.Н.

 

 

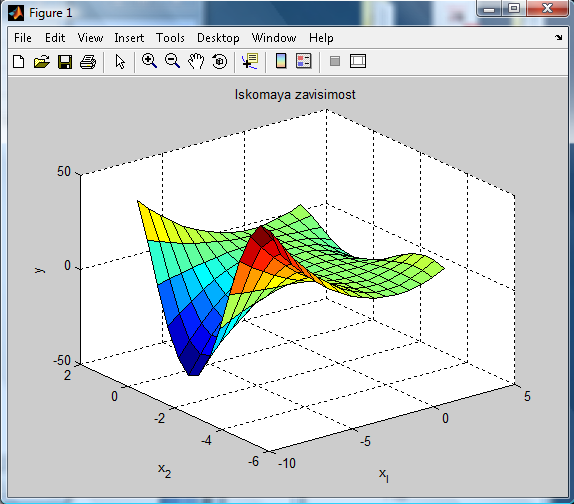
2012 г.

Задание: Создать систему нечёткого вывода типа Сугено, моделирующую зависимость в области Проектирование осуществить на основе трёхмерного изображения указанной зависимости (рис.1), которое построено следующей программой (рис.2):

рис.1

рис.2

 

 

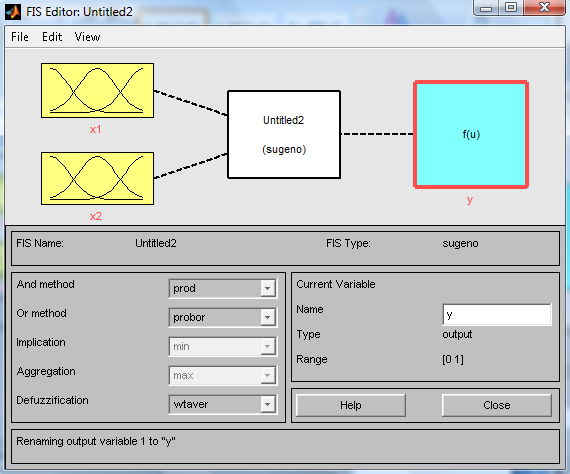
Выполнение:

1) Открыть FIS-редактор, напечатать слово fuzzy в командной строке. После этого появится новое графическое окно. Выберем тип системы. Для этого в меню File выбираем в подменю New FIS команду Sugeno (рис.3).

рис.3

2) Добавим вторую входную переменную (Меню Edit -> Команда Add input). Переименуем входные и выходные переменные (рис.4) и после этого зададим имя системы (рис.5).

рис.4

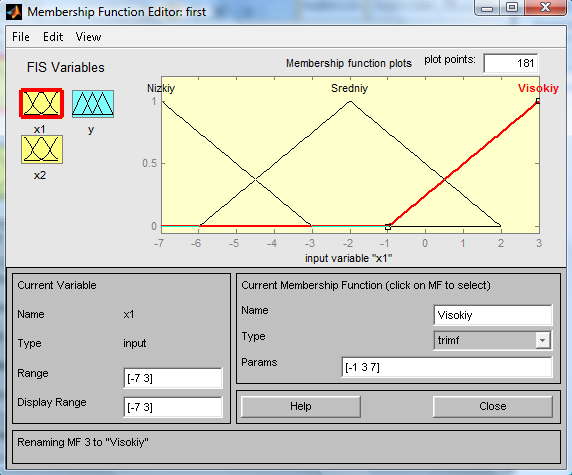
рис.5

3) Перейдём в редактор функций принадлежности (щелчок левой кнопкой мыши на блоке X1). Зададим диапазон изменения переменной X1, напечатав -7 3 в поле Range. Зададим функции принадлежности переменной X1. Для лингвистической оценки переменной будем использовать три терма с треугольными функциями принадлежности (функции установлены по умолчанию). Зададим наименования термов переменной X1. Обозначим их как Низкий, Средний, Высокий. В результате получим графическое окно, полученное на рис.6. Аналогично произведём задание функции принадлежности переменной X2.

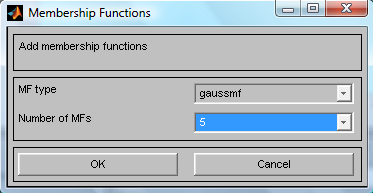
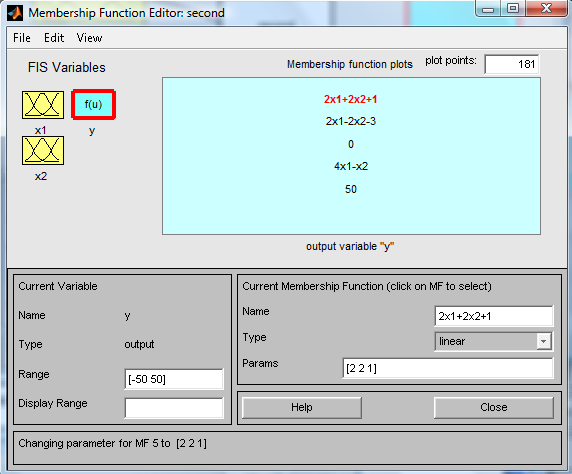
рис.6.

4) Для лингвистической оценки Y будем использовать пять термов с гауссовыми функциями принадлежности. Зададим диапазон -50 50 в поле Range. Затем в меню Edit выберем команду Remove All MFs для удаления установленных по умолчанию функций принадлежности. После этого в меню Edit выберем команду Add MFs. В появившемся окне выберем тип функции принадлежности gaussmf в поле MF type и пять термов в поле Number of MFs (рис.7).

рис.7

5) Дадим наименования термам переменной y. Зададим исключения из правил (рис.8).

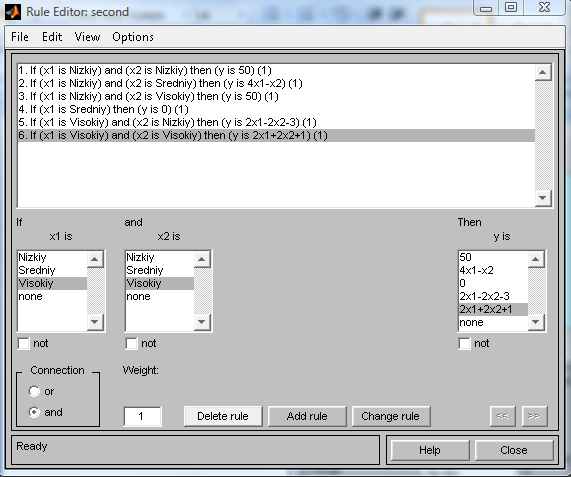
рис.8

6) Перейдём в редактор базы знаний RuleEditor. Для этого в меню Edit выберем команду Rules. Введём правила (рис9).

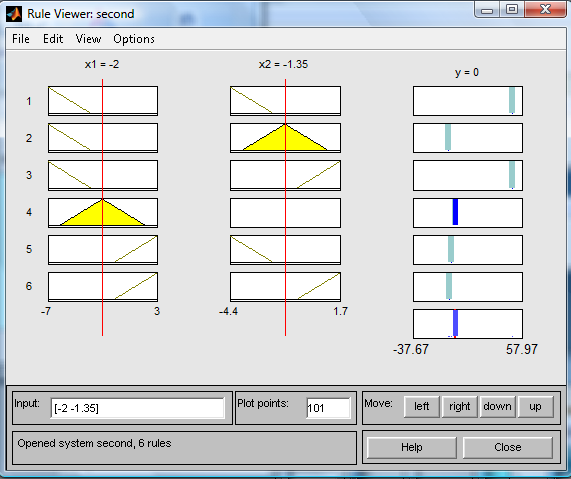
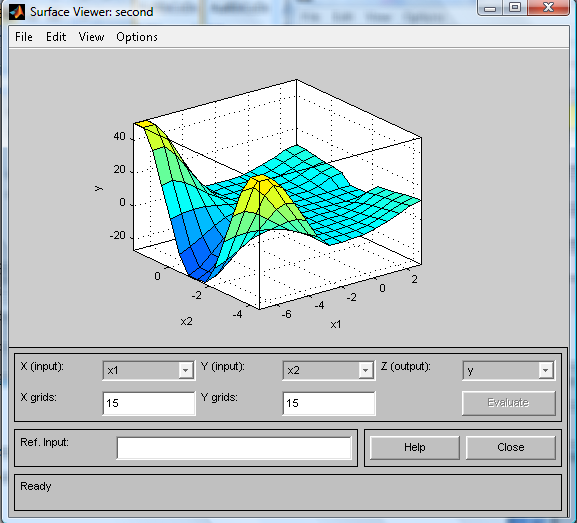
рис.9

7) Сохраним созданную систему. Для этого в меню File выберем в подменю Export команду To disk. Покажем окно визуализации нечёткого вывода (рис.10). Окно активируется командой Rules меню View. В поле Input указываются значения входных переменных, для которых выполняется нечёткий логический вывод. На рис.11 приведена поверхность «входы-выходы», соответствующая синтезированной нечёткой системе. Окно выводится по команде Surface меню View.

рис.10

рис.11

Сравнивая поверхности на рис.1 и рис.11, можно сделать вывод, что нечёткие правила описывают особенности моделируемой нелинейной зависимости.