СУГЕНО С ПОМОЩЬЮ ANFIS-РЕДАКТОРА

Лабораторная работа № 3

по дисциплине:

Прикладные нечёткие системы

на тему:

ЭКСТРАКЦИЯ ИЗ ДАННЫХ НЕЧЁТКОЙ СИСТЕМЫ

СУГЕНО С ПОМОЩЬЮ ANFIS-РЕДАКТОРА

 

Выполнил:

студент группы ВТМ-11

Соколов И.П.

Проверил:

доцент Боцула Л.Н.

 

 

2012 г.

Задание: Построить нечёткую систему типа Сугено из экспериментальных данных на примере моделирования зависимости ширины лепестка ириса от длины чашелистика и длины лепестка. Экспериментальные данные записаны в файле iris.dat, который содержит результаты измерения 150 ирисов. Ширина лепестка записана в четвёртом столбце, длина чашелистика – в первом столбце, а длина лепестка – в третьем.

Выполнение:

1) В обучающую выборку включим 120 ирисов, а в тестовую – 30. Для этого выполним следующие команды, по которым в рабочей области формируется обучающая выборка (tr_set) и тестовая выборка (test_set):

>> ir=load('iris.dat');

>> iris_number=length(ir);

>> test_index=[6:10:iris_number 7:10:iris_number];

>> tr_index=setdiff(1:iris_number, test_index);

>> tr_set=ir(tr_index, [1 3 4]);

>> test_set=ir(test_index, [1 3 4]).

Результаты:

test_set =   54 17 4 57 15 4 50 16 2 50 12 2 48 14 3 57 45 13 67 44 14 66 44 14 60 45 16 57 42 12 76 66 21 64 53 23 72 60 18 77 61 23 67 52 23 46 14 3 54 13 4 50 16 4 55 13 2 51 16 2 63 47 16 56 45 15 68 48 14 67 47 15 57 42 13 49 45 17 65 55 18 62 48 18 63 56 24 63 50 19

tr_set =   51 14 2 49 14 2 47 13 2 46 15 2 50 14 2 50 15 2 44 14 2 49 15 1 54 15 2 48 16 2 48 14 1 43 11 1 58 12 2 51 14 3 57 17 3 51 15 3 54 17 2 51 15 4 46 10 2 51 17 5 48 19 2 52 15 2 52 14 2 47 16 2 48 16 2 54 15 4 52 15 1 55 14 2 49 15 2 49 14 1 44 13 2 51 15 2 50 13 3 45 13 3 44 13 2 50 16 6 51 19 4 46 14 2 53 15 2 50 14 2 70 47 14 64 45 15 69 49 15 55 40 13 65 46 15 49 33 10 66 46 13 52 39 14 50 35 10 59 42 15 60 40 10 61 47 14 56 36 13 58 41 10 62 45 15 56 39 11 59 48 18 61 40 13 63 49 15 61 47 12 64 43 13 67 50 17 60 45 15 57 35 10 55 38 11 55 37 10 58 39 12 60 51 16 54 45 15 63 44 13 56 41 13 55 40 13 55 44 12 61 46 14 58 40 12 50 33 10 56 42 13 62 43 13 51 30 11 57 41 13 63 60 25 58 51 19 71 59 21 63 56 18 65 58 22 73 63 18 67 58 18 72 61 25 65 51 20 64 53 19 68 55 21 57 50 20 58 51 24 77 67 22 77 69 23 60 50 15 69 57 23 56 49 20 77 67 20 63 49 18 67 57 21 61 49 18 64 56 21 72 58 16 74 61 19 79 64 20 64 56 22 63 51 15 61 56 14 64 55 18 60 48 18 69 54 21 67 56 24 69 51 23 58 51 19 68 59 23 67 57 25 65 52 20 62 54 23 59 51 18

 

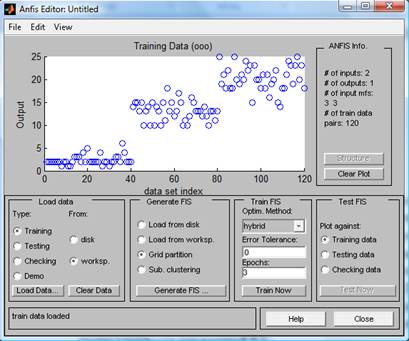
2) Командой anfisedit загрузим ANFIS-редактор (рис.1), в котором сгенерируем и обучим нечёткую систему типа Сугено. Для загрузки обучающей выборки в окне ANFIS-редактора в поле Load data выберем опцию Training (меню Type) и worksp. (меню From) и нажмём кнопку Load data...

рис.1

3) В результате появится окно (рис.2), в котором напечатаем идентификатор tr_set и нажмём ОК.

рис.2

Результат (рис.3):

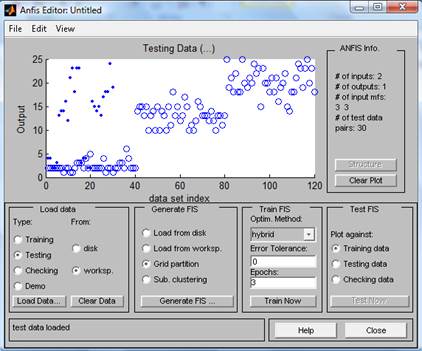
рис.3

4) Для загрузки тестовой выборки установим опцию Testing в меню Type, нажмём Load data… и в появившемся окне напечатать test_set. После этих действий ANFIS-редактор будет выглядеть как на рис. 4. Данные обучающей выборки показаны окружностями, а тестовой выборки – точками.

рис.4

5) Создадим систему нечёткого вывода, нажав кнопку Generate FIS… (рис.5). По умолчанию используется простой метод решётчатого разбиения (Grid partition), согласно которому функции принадлежности нечётких термов равномерно распределяются внутри диапазона изменения данных.

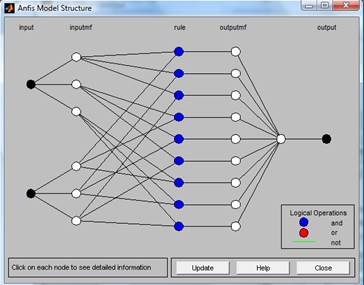
рис.5

6) Теперь с нечёткой логикой можно работать, используя GUI-модули пакета Fuzzy Logic Toolbox. Вызов этих модулей происходит через меню Edit и View. Для изображения синтезированной системы в виде нейро-нечёткой сети (рис.6) необходимо нажать кнопку Structure в поле ANFIS Info.

рис.6

7) Проведём обучение нечёткой системы на 25 итераций. Для этого в поле Epochs: меню Train FIS напечатаем «25» и нажмём кнопку Train now. Динамика обучения выводится в основном окне ANFIS-редактора (рис. 7): ось абсцисс соответствует итерациям алгоритма обучения, а ось ординат – значениям очередной квадратичной оценки. После настройки ошибка обучения составляет примерно 1,8.

рис.7

8) Для проверки модели на тестовой выборке установим в поле Test FIS опцию Testing data и нажмём Test Now. Результаты тестирования выводятся в основном окне ANFIS-редактора (рис. 8). Экспериментальные данные показаны точками, а результаты моделирования – звёздочками. Ошибка тестовой выборки составляет примерно 1,9.

рис.8

9) Сохраним на диске нечёткую систему: File -> Export -> To disk (рис.9)

рис.9

10) Сравним результаты нечёткой идентификации с линейной и квадратичной регрессиями. Идентификацию параметров линейной модели x4=a0+a1x1+a2x3 осуществим следующими командами:

>> N=length(tr_set);

>> NN=length(test_set);

>> disp('Lineinaya model:')

Lineinaya model:

>> X=[ones(N,1) tr_set(:,1) tr_set(:,2)];

>> A=X\tr_set(:,3)

A =

0.3730

-0.0975

0.4578

>> %Raschet nevyazki na obuchauschey viborke

>> Out_model=X*A;

>> rmg_tr=norm(tr_set(:,3)-Out_model)/sqrt(N)

rmg_tr =

2.0158

>> %Raschet nevyazki na testovoy viborke

>> X_test=[ones(NN,1) test_set(:,1) test_set(:,2)];

>> Out_model=X_test*A;

>> rmg_ch=norm(test_set(:,3)-Out_model)/sqrt(NN)

rmg_ch =

2.0783

В результате получаем модель: x4=0,373-0,098x1+0,458x3, ошибки которой на обучающей и тестовой выборке составляют 2,02 и 2,08 соответственно.

11) Для идентификации параметров нелинейной модели x4=a0+a1x1+a2x3+a3x1^2+a4x3^2+a5x1x3 выполним следующие команды:

>> disp('Kvadratichnaya model:')

Kvadratichnaya model:

>> X=[ones(N,1) tr_set(:,1) tr_set(:,2) tr_set(:,1).^2 tr_set(:,2).^2 tr_set(:,1).*tr_set(:,2)];

>> A=X\tr_set(:,3)

A =

-25.5640

0.8696

0.3142

-0.0078

0.0035

-0.0017

>> Out_model=X*A;

>> rmg_tr=norm(tr_set(:,3)-Out_model)/sqrt(N)

rmg_tr =

1.9414

>> X_test=[ones(NN,1) test_set(:,1) test_set(:,2) test_set(:,1).^2 test_set(:,2).^2 test_set(:,1).*test_set(:,2)];

>> Out_model=X_test*A;

>> rmg_ch=norm(test_set(:,3)-Out_model)/sqrt(NN)

rmg_ch =

1.9923

В результате получаем модель:

x4 = -25,564+0,87x1+0,314x3-0,008x1^2+0,004x3^2-0,002x1x3, ошибки которой на обучающей и тестовой выборках составляют 1,94 и 1,99 соответственно.

Таким образом, нечёткая модель точнее линейной и квадратичной регрессий описывает зависимость ширины лепестка от длины чашелистика и длины лепестка.