Решение.
Интегрирование методом подстановки.
Очень часто метод подстановки выручает при интегрировании тригонометрических функций и функций с радикалами.
Найти неопределенный интеграл Решение. Введем новую переменную
Выполняем подстановку полученных выражений в исходный интеграл:
Из таблицы первообразных имеем Осталось вернуться к исходной переменной х:
Ответ: Неопределённый интегра́л для функции Если функция
где С — произвольная постоянная.
Если
|
.
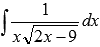. Выразим х через z:
.
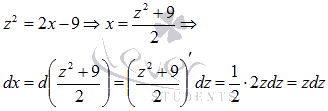
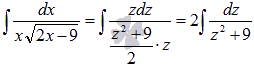
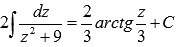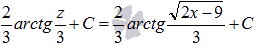
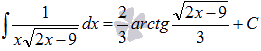
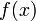— это совокупность всех первообразных данной функци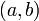и.
и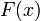 
— её первообразная, то есть 
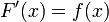при 
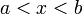, то
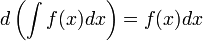
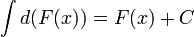
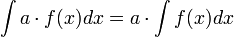
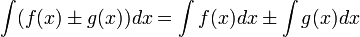
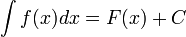, то и 
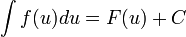, где 
— произвольная функция, имеющая непрерывную производную
