Метод касательных
Пусть функция f(x) определена и непрерывна на [a, b]. Пусть на [a, b] есть корень и только один, т. е. f(a)*f(b)<0, график функции проходит через точку A(a, f(a)), B(b, f(b)) и f’(x), f’’(x) знакопостоянны на [a, b].
В точке B(b, f(b)) проводим касательную. Уравнение касательной запишется так:
Для нахождения точки пересечения этой прямой с осью Ox нужно принять y=0, а x=x1, тогда получаем: 0=f(b)+f’(b)(x1-b) f’(b)(x1-b)=- f(b)
Если касательная проведена в точку B(b, f(b)), то получаем x1, найдя значение x1 по формуле, вычислим x1 и найдём точку B1(x1, f(x1)), тогда
Процесс продолжается неограниченно. x1,…, xn являются приближёнными значениями корня. Замечание. Для того, чтобы точка пересечения касательной с осью Ox лежала внутри [a, b] касательную надо проводить через тот конец отрезка [a, b], где знак функции и второй производной совпадают. Методами математического анализа можно доказать, что последовательность x1,…, xn есть последовательность приближённых значений корня, она монотонна, сходится и её предел равен истинному значению корня, процесс закончить, когда |xn+1-xn|< ε;.
f(x)=x3-28x+48=0, [3;7], ε=0,01 Метод половинного деления: c1=(a+b)/2=5, [3;5] [5;7]
f(5)·f(7)>0 – не подходит, т.к. f(3)=-9, f(5)=33, f(7)=195 Имеем отрезок [3;5] c2=4, [3;4], [4;5] т.к. f(4)=0, c2=4 – искомый корень. Метод хорд: Точка пересечения хорды с осью c1=a-((f(a)·(b-a)/(f(b)-f(a)))=3-((-9·(7-3))/(195+9))=3,088, [3;3,088] [3,088;7]
f(3,088)·f(7)<0 – не подходит, т.к. f(3)=-9, f(3,088)=-9,016, f(7)=195 c2=c1-((f(c1)·(b- c1)/(f(b)-f(c1)))=3,088-((-9,016·(7-3,088))/(195+9,016))=3,262, [3,088;3,262] [3,262;7]
f(3,262)·f(7)<0 – не подходит, т.к. f(3,088)=-9,016, f(3,262)=-8,594, f(7)=195 c3=3,425, [3,262;3,425] [3,425;7]
f(3,425)·f(7)<0 – не подходит, т.к. f(3,262)=-8,594, f(3,425)=-7,686, f(7)=195 c4=3,565, [3,425;3,565] [3,565;7]
f(3,565)·f(7)<0 – не подходит, т.к. f(3,425)=-7,686, f(3,565)=-6,461, f(7)=195 c5=3,679, [3,565;3,679] [3,679;7]
f(3,679)·f(7)<0 – не подходит, т.к. f(3,565)=-6,461, f(3,679)=-5,204, f(7)=195 c6=3,766, [3,679;3,766] [3,766;7]
f(3,766)·f(7)<0 – не подходит, т.к. f(3,679)=-5,204, f(3,766)=-3,977, f(7)=195 c7=3,835, [3,766;3,835] [3,835;7]
f(3,835)·f(7)<0 – не подходит, т.к. f(3,766)=-3,977, f(3,835)=-2,897, f(7)=195 c8=3,886, [3,835;3,886] [3,886;7]
f(3,886)·f(7)<0 – не подходит, т.к. f(3,835)=-2,897, f(3,886)=-2,056, f(7)=195 c9=3,923, [3,886;3,923] [3,923;7]
f(3,923)·f(7)<0 – не подходит, т.к. f(3,886)= -2,056, f(3,923)=-1,524, f(7)=195 c10=3,944, [3,923;3,944] [3,944;7]
f(3,944)·f(7)<0 – не подходит, т.к. f(3,923)= -1,524, f(3,944)=-1,157, f(7)=195 c11=3,958, [3,944;3,958] [3,958;7]
f(3,958)·f(7)<0 – не подходит, т.к. f(3,944)= -1,157, f(3,958)=-0,781, f(7)=195 c12=3,972, [3,958;3,972] [3,972;7]
f(3,972)·f(7)<0 – не подходит, т.к. f(3,958)= -0,781, f(3,972)=-0,589, f(7)=195 c13=3,979, т.к. |c13-c12|=0.007< ε, c13=3,979 – искомый корень. Метод касательных: f(x)=x3-28x+48=0, [3;7], ε=0,01 f’(x)=3x2-28 c0=7, c1=c0-f(c0)/f’(c0), f(7)=195, f’(7)=119, c1=7-195/119=5,361; f(5,361)=51,911, f’(5,361)=58,189, c2=5,361-51,911/58,189=4,47; f(4,47)=12,155, f’(4,47)=31,943, c3=4,09; f(4,09)=1,898, f’(4,09)=22,184, c4=4,004; f(4,004)=0,080, f’(4,004)=20,096, c5=4 т.к. |c5-c4|=0.004< ε, c5=4 – искомый корень. program lab1 real a, b, e, x real f f(x)=x**3-28.*x+48. a=3. b=7. e=0,01 do while (asb(b-a)>=e) x=(b-a)/2. if (f(x)==0.) exit if (f(a)*f(x)<0.) then b=x else a=x end if end do write (*,*) ‘x=’,x read (*,*) end program lab1
|



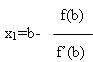

 f(3)·f(5)<0 – подходит;
f(3)·f(5)<0 – подходит;


