Структурные схемы цифровых фильтров
Алгоритмы цифровой фильтрации сигналов (цифровых фильтров) представляются в виде структурных схем, базовые элементы которых показаны на рис 1.7 вместе с примерами структурных схем фильтров. Как правило, структурные схемы соответствуют программной реализации фильтров на ЭВМ, но не определяют аппаратной реализации в специальных радиотехнических устройствах, которая может существенно отличаться от программной реализации.
Соединения фильтров. Различают следующие соединения фильтров.
1. Последовательное соединение (рис 1.8). Выходной сигнал предшествующего фильтра является входным для последующего. Эквивалентная передаточная функция общей системы равна произведению передаточных функций фильтров, в нее входящих: H(z) = H1(z)×H2(z)×HN(z).
2. Параллельное соединение (рис 1.9). Сигнал подается на входы всех параллельно соединенных фильтров одновременно, выходные сигналы фильтров суммируются. Эквивалентная передаточная функция общей системы равна сумме передаточных функций фильтров, в нее входящих: H(z) = H1(z)+H2(z)+...+HN(z).
3. Соединение обратной связи (рис 1.10). Выходной сигнал первого фильтра подается на выход системы и одновременно на вход фильтра обратной связи, выходной сигнал которого суммируется, со знаком плюс или минус в зависимости от вида связи (отрицательной или положительной), с входным сигналом системы. Эквивалентная передаточная функция системы: H(z) = H1(z)/(1±H1(z)H2(z)).
Схемы реализации фильтров.По принципам структурной реализации фильтров различают следующие схемы: 1. Прямая форма (рис 1.11) реализуется непосредственно по разностному уравнению: yk = или по передаточной функции: H(z) = 2. Прямая каноническая форма содержит минимальное число элементов задержки. Передаточную функцию РЦФ можно представить в следующем виде: H(z) = Y(z)/X(z) = H1(z)H2(z); H1(z) = V(z)/X(z) = 1/(1+ Отсюда: v(k) = x(k) - y(k) = В разностных уравнениях (1.10-1.11) осуществляется только задержка сигналов v(k). 3. Каскадная (последовательная) форма соответствует представлению передаточной функции в виде произведения: H(z) = Hi(z) - составляющие функции вида (1-riz)/(1-piz) при представлении H(z) в факторизованной форме, где ri и pi - нули и полюсы функции H(z). В качестве функций Hi(z) обычно используются передаточные функции биквадратных блоков - фильтров второго порядка: Hi(z) = (b0i + b1i ×z + b2i ×z2) / (1 + a1i ×z + a2i ×z2). 4. Параллельная форма используется много реже, и соответствует представлению передаточной функции в виде суммы биквадратных блоков или более простых функций.
|

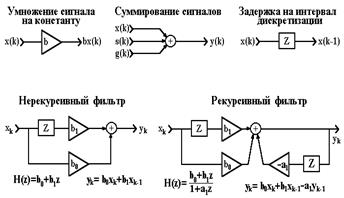 Рисунок 1.7 Структурные схемы цифровых фильтров.
Рисунок 1.7 Структурные схемы цифровых фильтров.
 Рисунок 1.8
Рисунок 1.8
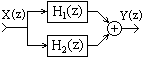 Рисунок 1.9
Рисунок 1.9
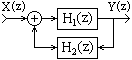 Рисунок 1.10
Рисунок 1.10
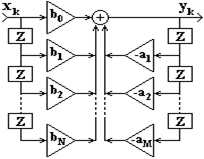 Рисунок 1.11
Рисунок 1.11
 bnxk-n –
bnxk-n – 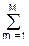 amyk-m,
amyk-m,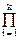 Hi(z).
Hi(z).


