Пояснения к работе. Трехфазная система электрических цепей – совокупность электрических цепей, в которых действуют три синусоидальные ЭДС одной и той же частоты
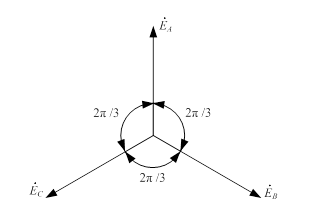
Трехфазная система электрических цепей – совокупность электрических цепей, в которых действуют три синусоидальные ЭДС одной и той же частоты, сдвинутые друг относительно друга по фазе и создаваемые общим источником энергии. Если все три ЭДС равны по значению и сдвинуты по фазам на 120о, то такая система называется симметричной.
а)
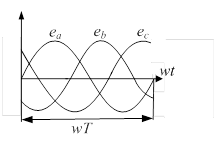
б) Рисунок 1.1 - Трехфазная симметричная система ЭДС а) векторная диаграмма; б) временная диаграмма
Если эти условия не соблюдаются, то система ЭДС не симметрична. Аналогично определяются трехфазные системы напряжений и токов. Часть трехфазной системы электрических цепей, в которой может протекать один из токов трехфазной системы, называется фазой. Таким образом, фазой являются обмотка генератора, в которой индуктируется ЭДС и приемник, присоединенный к этой обмотке. Это второе значение термина «фаза», которое широко используется в практической электротехнике. Если принять, что для ЭДС фазы А начальная фаза, равняется нулю, то мгновенные значения фазных ЭДС:
Комплексы действующих значений
При симметричной системе ЭДС
При соединении «звездой» (рис.1.2.) концы фаз генератора или приемника соединены в один узел. Провода А-а; В-b; C-c,соединяющие начала фаз генератора и приемника, называются линейными. Линейное напряжение – это напряжение между линейными проводами (
Рисунок 1.2 - Схема четырех проводной трехфазной цепи
Имеют место соотношения, которые удобно использовать при построении векторных диаграмм:
Для симметричной системы
Ток в нейтральном проводе в несимметричном режиме может быть определен из уравнения по первому закону Кирхгофа для точки n:
При симметричной нагрузке Ток в каждой фазе может быть определен по закону Ома:
где Аналогично определяют фазные токи İb и İc. Зная величину токов Ia; Ib; Ic и сдвиги фаз φ a; φ b; φ c между векторами соответствующих фаз напряжений и токов, можно построить векторную диаграмму (рис. 1.3).
Рисунок 1.3 - Векторная диаграмма напряжений и токов при несимметричной нагрузке
При построении векторной диаграммы принято, что система фазных напряжений симметрична (что почти всегда реально на практике), а сопротивления фаз приемников различны. В результате фазные токи оказываются различными по величине и сдвинутыми по фазе на различные углы. Вектор İn находят геометрическим сложением фазных токов. При отсутствии нейтрального провода (в трехпроводной трехфазной системе) симметричный режим ничем не отличается от соответствующего режима в четырехпроводной системе.
Рисунок 1.4 - Схема трехпроводной трехфазной цепи при соединении нагрузки в «звезду»
При несимметричной нагрузке появляется "смещение нейтрали" – разность потенциалов между нейтральными точками генератора и приемника UNn, что приводит к изменению фазных напряжений ("перекос фаз"):
где
Фазные напряжения определяются по второму закону Кирхгофа для трех контуров
Такой режим крайне неблагоприятен, так как увеличение или уменьшение напряжения может привести к порче оборудования, или к работе его с некачественными характеристиками. Активной мощностью трехфазной системы называется сумма активных мощностей всех фаз источника энергии, равная сумме активных мощностей фаз приемника. В симметричной трехфазной системе при любом соединении фаз
фазная мощность
где φ– угол сдвига фаз между фазным напряжением и током. При несимметричной нагрузке
Реактивная мощность трехфазной системы - это сумма реактивных мощностей всех фаз:
Для симметричной системы
Полная мощность трехфазной системы
Сопротивление фаз определяется по формуле:
|

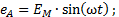 (1.1)
(1.1)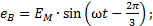 (1.2)
(1.2) (1.3)
(1.3)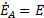 ;
;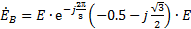

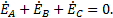
 ,
, 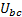 ,
,  ). Фазные напряжения - (
). Фазные напряжения - ( ,
, 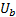 ,
, 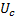 ) напряжения на фазе приемника. Линейный ток – ток в линейном проводе. Фазный ток – ток в фазе приемника.
) напряжения на фазе приемника. Линейный ток – ток в линейном проводе. Фазный ток – ток в фазе приемника.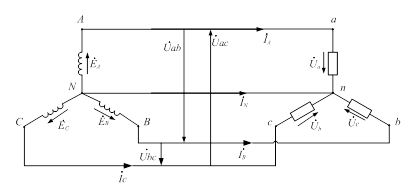
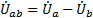 (1.8)
(1.8)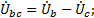 (1.9)
(1.9) (1.10)
(1.10)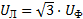 ;
;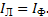
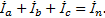
 .
.
 ;
; 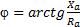 .
.

 (1.16)
(1.16) ,
, 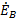 ,
,  - комплексы фазных ЭДС;
- комплексы фазных ЭДС;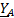 ,
, 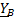 ,
, 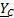 - комплексы фазных проводимостей.
- комплексы фазных проводимостей.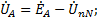
 ;
;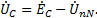
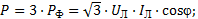 (1.17)
(1.17) (1.18)
(1.18)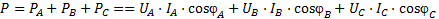

 (1.19)
(1.19)
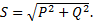
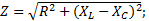 (1.22)
(1.22) (1.23)
(1.23)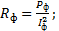 (1.24)
(1.24) (1.25)
(1.25)


