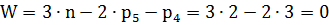Задачи синтеза рычажного механизма.
При синтезе рычажных механизмов стоят две задачи: метрический синтез недостающих размеров звеньев и вторая задача проектирование маховика, который необходимо установить на входном звене рычажного механизма с целью уменьшения колебаний угловой скорости входного звена. Синтез любого механизма включает в себя три этапа: 1. выбор и метрический синтез кинематической схемы механизма, которая обеспечивает требуемый вид и закон движения; 2. разработка конструктивных форм механизма, обеспечивающая прочность, долговечность, высокий КПД; 3. разработка технологических и технико-экономических показателей проектируемого механизма. Следует отметить, что в ТММ при рассмотрении первого этапа, также учитываются некоторые вопросы, связанные со вторым и третьем этапами. Задачей метрического синтеза является определение длин звеньев рычажного механизма. В данном механизме длины звеньев рычажного механизма известны. В период установившегося движения в реальной машине ω не остается постоянным, а колеблется относительно некоторого среднего значения. При решении 2-ой задачи за основное условие принимаем коэффициент неравномерности хода машины:
Где
Коэффициент Сравнительной оценкой динамических свойств машины в период установившегося движения является коэффициент динамичности:
Рисунок 1.1 – Динамика колебания угловой скорости в период установившегося движения.
По коэффициенту
1.3. Структурный анализ рычажного механизма.
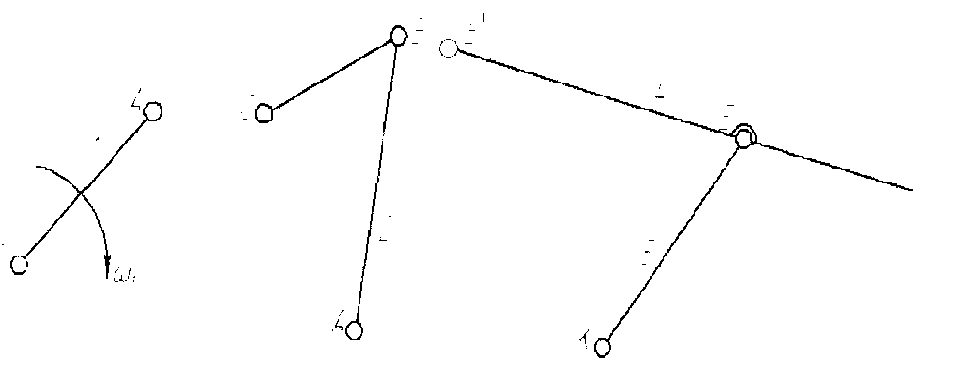
Механизмом называется система тел предназначенных для преобразования движения одних твердых тел в требуемое движение других твердых тел. Схематически изобразим механизм и обозначим на схеме (рис2.1) звенья и кинематические пары. Под звеном понимают одно тело или несколько тел жестко соединенных между собой. Кинематическая пара- соединение двух звеньев допускающее их относительное движение. Кинематической цепью - система звеньев, связанных между собой кинематическими парами. Кинематическая цепь, которая будучи подсоединенная к стойке имеет степень свободы 0 - называется структурной группой. Класс структурной группы определяется по числу внутренних кинематических пар в замкнутом контуре входящим в состав группы. Порядок структурной группы определяется по числу внешних кинематический пар в составе группы. Класс и порядок механизма определяют по классу и порядку старшей структурной группы. Сначала определяют какой механизм (плоский или пространственный), потом определяют число степеней свободы механизма, т.е. определяют число входных звеньев в механизме по формуле Чебушева для плоских механизмов, а по формуле Сомова-Малышева для пространственных, после строится заменяющая схема.
Рисунок 2. – Схема рычажного механизма.
Механизм, состоящий только из низших кинематических пар, т.е. в таких кинематических парах, в которых соприкосновение звеньев осуществляется по поверхности (вращательные, поступательные, цилиндрические или сферические), называют рычажным.
Для подсчета степени свободы пространственных механизмов применяют формулу Где
Для плоских механизмов Рычажный механизм представленный на рисунке 2.1 является плоским и значит, степень свободы подсчитываем по формуле Чебышева:
Степень свободы механизма равняется 1, следовательно, в механизме одно входное звено. Строим Заменяющую схему механизма, с указанием на структурные группы для чего: · Ползуны, кулисные камни, звенья другой конфигурации заменяем рычагами. · Поступательные пары заменяются вращательными. · Звенья которые соединяются с 3-мя другими звеньями изображается в виде треугольника, с 4-мя в виде четырехугольника. Чтобы разделить на механизм на структурные группы надо: · Отделить механизм первого класса. · Оставшуюся часть делить на наиболее простые структурные группы. За входное звено принимают звено1.
Рисунок 2.2 – Заменяющая схема рычажного механизма с указанием на структурные группы.
Структурные группы в отсоединенном виде:
|

 (1.2.1)
(1.2.1) - коэффициент неравномерности хода машины;
- коэффициент неравномерности хода машины; - максимальная угловая скорость в цикле;
- максимальная угловая скорость в цикле; - минимальная угловая скорость в цикле;
- минимальная угловая скорость в цикле;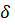 характеризует только перепад угловой скорости входного звена, но не характеризует динамики движения этого звена внутри этого цикла.
характеризует только перепад угловой скорости входного звена, но не характеризует динамики движения этого звена внутри этого цикла.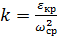 (1.2.2)
(1.2.2)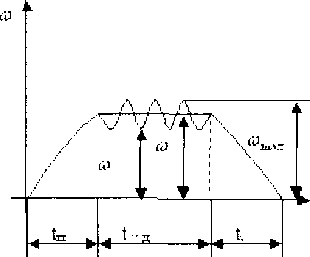
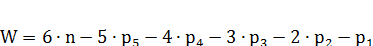 (формула Сомова-Малышева), стр38[1].
(формула Сомова-Малышева), стр38[1]. – число подвижных звеньев;
– число подвижных звеньев; – число одноподвижных кинематических пар;
– число одноподвижных кинематических пар; – число двухподвижных кинематических пар;
– число двухподвижных кинематических пар; – число трехподвижных кинематических пар;
– число трехподвижных кинематических пар; – число четырехподвижных кинематических пар;
– число четырехподвижных кинематических пар; – число пятиподвижных кинематических пар;
– число пятиподвижных кинематических пар;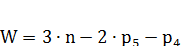 (формула Чебышева). Стр 38[1]
(формула Чебышева). Стр 38[1]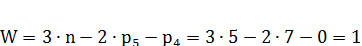

 . Значит данный механизм второго класса и второго порядка.
. Значит данный механизм второго класса и второго порядка.