Наряду с изучением вариации признака по всей совокупности в целом, становится возможным изучить вариацию для каждой из составляющих ее группы, а также и между этими группами. В простейшем случае, когда совокупность расчленена на группы по одному фактору, изучение вариации достигается посредством исчисления и анализа трех видов дисперсий: общей, межгрупповой и внутригрупповой. Общая дисперсия  измеряет вариацию признака по всей совокупности под влиянием всех факторов, обусловивших эту вариацию. Она равна среднему квадрату отклонений отдельных значение признака х от общей средней величины и может быть вычислена как простая дисперсия
измеряет вариацию признака по всей совокупности под влиянием всех факторов, обусловивших эту вариацию. Она равна среднему квадрату отклонений отдельных значение признака х от общей средней величины и может быть вычислена как простая дисперсия 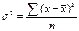 или взвешенная дисперсия
или взвешенная дисперсия  . Межгрупповая дисперсия
. Межгрупповая дисперсия 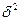 характеризует систематическую вариацию результативного признака, обусловленную влиянием признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений групповых (частных) средних
характеризует систематическую вариацию результативного признака, обусловленную влиянием признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений групповых (частных) средних  от общей средней
от общей средней  :
:  , где f – численность единиц в группе. Внутригрупповая (частная) дисперсия
, где f – численность единиц в группе. Внутригрупповая (частная) дисперсия 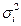 отражает случайную вариацию неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировка. Она равна среднему квадрату отклонений отдельных значений признака внутри группы х от средней арифметической этой группы xi (групповой средней) и может быть исчислена как простая дисперсия
отражает случайную вариацию неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировка. Она равна среднему квадрату отклонений отдельных значений признака внутри группы х от средней арифметической этой группы xi (групповой средней) и может быть исчислена как простая дисперсия  или как взвешенная дисперсия
или как взвешенная дисперсия  . На основании внутригрупповой дисперсии по каждой группе, т.е. на основании
. На основании внутригрупповой дисперсии по каждой группе, т.е. на основании 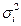 можно определить общую среднюю из внутригрупповых дисперсий:
можно определить общую среднюю из внутригрупповых дисперсий:  . Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий:. Пользуясь правилом сложения дисперсий, можно всегда по двум известным дисперсиям определить третью – неизвестную. Чем больше доля межгрупповой дисперсии в общей дисперсии, тем сильнее влияние группировочного признака на изучаемый признак. Поэтому в статистическом анализе широко используется эмпирический коэффициент детерминации
. Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий:. Пользуясь правилом сложения дисперсий, можно всегда по двум известным дисперсиям определить третью – неизвестную. Чем больше доля межгрупповой дисперсии в общей дисперсии, тем сильнее влияние группировочного признака на изучаемый признак. Поэтому в статистическом анализе широко используется эмпирический коэффициент детерминации  - показатель, представляющий собой долю межгрупповой дисперсии в общей дисперсии результативного признака и характеризующий силу влияния группировочного признака на образование общей вариации:
- показатель, представляющий собой долю межгрупповой дисперсии в общей дисперсии результативного признака и характеризующий силу влияния группировочного признака на образование общей вариации:  . При отсутствии связи эмпирический коэффициент детерминации равен нулю, а при функциональной связи – единице. Эмпирическое корреляционное отношение – это корень квадратный из эмпирического коэффициента детерминации:
. При отсутствии связи эмпирический коэффициент детерминации равен нулю, а при функциональной связи – единице. Эмпирическое корреляционное отношение – это корень квадратный из эмпирического коэффициента детерминации: 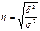 . Он показывает тесноту связи между группировочным и результативным признаками. Эмпирическое корреляционное отношение может принимать значения от 0 до 1. Если связь отсутствует, то корреляционное отношение равно нулю, т.е. все групповые средние будут равны между собой, межгрупповой вариации не будет. Значит, группировочный признак никак не влияет на образование общей вариации. Если связь функциональная, то корреляционное отношение будет равно единице. В этом случае дисперсия групповых средних равна общей дисперсии
. Он показывает тесноту связи между группировочным и результативным признаками. Эмпирическое корреляционное отношение может принимать значения от 0 до 1. Если связь отсутствует, то корреляционное отношение равно нулю, т.е. все групповые средние будут равны между собой, межгрупповой вариации не будет. Значит, группировочный признак никак не влияет на образование общей вариации. Если связь функциональная, то корреляционное отношение будет равно единице. В этом случае дисперсия групповых средних равна общей дисперсии  , т.е. внутригрупповой вариации не будет. Это означает, что группировочный признак целиком определяет вариацию изучаемого результативного признака. Чем значение корреляционного отношения ближе к единице, тем теснее, ближе к функциональной зависимости связь между признаками.
, т.е. внутригрупповой вариации не будет. Это означает, что группировочный признак целиком определяет вариацию изучаемого результативного признака. Чем значение корреляционного отношения ближе к единице, тем теснее, ближе к функциональной зависимости связь между признаками.
20. Выборочное наблюдение: основные понятия, цель, принцип, необходимость применения. Использование выборочного наблюдения в статистической практике.
Выборочное наблюдение – несплошное наблюдение, при котором обследованию подвергается часть совокупности, отобранная в случайном порядке, а результаты представляют всю совокупность
Виды:
· Индивидуальный (по 1 единице)
· Групповой (группа)
· Комбинированный (индивидуальный + групповой)
Методы отбора:
· Повторный
· Бесповторный
Способы отбора:
· По степени охвата:
-большие
-малые
· По виду:
- собственно – случайная: всем единицам генеральной совокупности присваивается номер и на каждую единицу заводится жребий, используют таблицу случайных чисел
- механическая (только бесповторный): в генеральную совокупность отбирается каждый n/N элемент совокупности
- типическая: генеральная совокупность разбивается по существенным признакам на классы или типы, затем из полученных классов происходит отбор в выборочную совокупность осуществляется пропорционально численности этих типов
- серийный проводится в два этапа:
ü 1 этап: в случайном порядке выбираются группы единиц
ü 2 этап: каждая единица выбранных групп изучается
- комбинированный: сочетает в себе 2 или более из перечисленных типов
21. Способы формирования выборочной совокупности, виды отбора.

 измеряет вариацию признака по всей совокупности под влиянием всех факторов, обусловивших эту вариацию. Она равна среднему квадрату отклонений отдельных значение признака х от общей средней величины и может быть вычислена как простая дисперсия
измеряет вариацию признака по всей совокупности под влиянием всех факторов, обусловивших эту вариацию. Она равна среднему квадрату отклонений отдельных значение признака х от общей средней величины и может быть вычислена как простая дисперсия 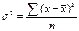 или взвешенная дисперсия
или взвешенная дисперсия  . Межгрупповая дисперсия
. Межгрупповая дисперсия 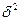 характеризует систематическую вариацию результативного признака, обусловленную влиянием признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений групповых (частных) средних
характеризует систематическую вариацию результативного признака, обусловленную влиянием признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений групповых (частных) средних  от общей средней
от общей средней  :
:  , где f – численность единиц в группе. Внутригрупповая (частная) дисперсия
, где f – численность единиц в группе. Внутригрупповая (частная) дисперсия 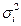 отражает случайную вариацию неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировка. Она равна среднему квадрату отклонений отдельных значений признака внутри группы х от средней арифметической этой группы xi (групповой средней) и может быть исчислена как простая дисперсия
отражает случайную вариацию неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировка. Она равна среднему квадрату отклонений отдельных значений признака внутри группы х от средней арифметической этой группы xi (групповой средней) и может быть исчислена как простая дисперсия  или как взвешенная дисперсия
или как взвешенная дисперсия  . На основании внутригрупповой дисперсии по каждой группе, т.е. на основании
. На основании внутригрупповой дисперсии по каждой группе, т.е. на основании  . Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий:. Пользуясь правилом сложения дисперсий, можно всегда по двум известным дисперсиям определить третью – неизвестную. Чем больше доля межгрупповой дисперсии в общей дисперсии, тем сильнее влияние группировочного признака на изучаемый признак. Поэтому в статистическом анализе широко используется эмпирический коэффициент детерминации
. Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий:. Пользуясь правилом сложения дисперсий, можно всегда по двум известным дисперсиям определить третью – неизвестную. Чем больше доля межгрупповой дисперсии в общей дисперсии, тем сильнее влияние группировочного признака на изучаемый признак. Поэтому в статистическом анализе широко используется эмпирический коэффициент детерминации  - показатель, представляющий собой долю межгрупповой дисперсии в общей дисперсии результативного признака и характеризующий силу влияния группировочного признака на образование общей вариации:
- показатель, представляющий собой долю межгрупповой дисперсии в общей дисперсии результативного признака и характеризующий силу влияния группировочного признака на образование общей вариации:  . При отсутствии связи эмпирический коэффициент детерминации равен нулю, а при функциональной связи – единице. Эмпирическое корреляционное отношение – это корень квадратный из эмпирического коэффициента детерминации:
. При отсутствии связи эмпирический коэффициент детерминации равен нулю, а при функциональной связи – единице. Эмпирическое корреляционное отношение – это корень квадратный из эмпирического коэффициента детерминации: 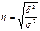 . Он показывает тесноту связи между группировочным и результативным признаками. Эмпирическое корреляционное отношение может принимать значения от 0 до 1. Если связь отсутствует, то корреляционное отношение равно нулю, т.е. все групповые средние будут равны между собой, межгрупповой вариации не будет. Значит, группировочный признак никак не влияет на образование общей вариации. Если связь функциональная, то корреляционное отношение будет равно единице. В этом случае дисперсия групповых средних равна общей дисперсии
. Он показывает тесноту связи между группировочным и результативным признаками. Эмпирическое корреляционное отношение может принимать значения от 0 до 1. Если связь отсутствует, то корреляционное отношение равно нулю, т.е. все групповые средние будут равны между собой, межгрупповой вариации не будет. Значит, группировочный признак никак не влияет на образование общей вариации. Если связь функциональная, то корреляционное отношение будет равно единице. В этом случае дисперсия групповых средних равна общей дисперсии  , т.е. внутригрупповой вариации не будет. Это означает, что группировочный признак целиком определяет вариацию изучаемого результативного признака. Чем значение корреляционного отношения ближе к единице, тем теснее, ближе к функциональной зависимости связь между признаками.
, т.е. внутригрупповой вариации не будет. Это означает, что группировочный признак целиком определяет вариацию изучаемого результативного признака. Чем значение корреляционного отношения ближе к единице, тем теснее, ближе к функциональной зависимости связь между признаками.


