Модель медицинского страхования компании

Исходные данные			Допущения
Количество служащих		N	Увеличение	dN%	в месяц
Индив. месяч. потребн.		zc	Увеличение	dzc%	в месяц
Индив. месяч. взнос		mo	Не изменяется
Месяц	Кол-во служащих	Месячные взносы	Инд. мес. пот-ть	Мес. потребность		Доплата компании
	N*(1+dN/100)	Кол-во служащих*mo	zc*dzc	Кол-во служащих*инд.мес.потребн		(Мес. потребность) – (Мес. взносы)

....

ИТОГО						????

Таким образом, количество служащих в любой заданный месяц бу­дет определяться следующим выражением: Количество служащих в данном месяце = Количество служащих в предшествующем месяце *(1+а/100+(b/100-а/100)* СЛЧИС()).

Допустим, что индивидуальная среднемесячная потребность в медицинских услугах представляет собой нормально распределенную случайную перемен­ную с параметрами: средним значением μ; (в нашем случае μ; = zc) и среднеквадратическим отклонением σ;. Причем в рассматриваемом случае среднее значение μ; увеличивается на dzc % в месяц, а среднеквадратическим отклонением σ; примерно равно 3%. Это будет соответствовать среднему увеличению общей месячной потребности в медицинских услугах от одного месяца до другого в dzc %.

По сделанным нами допущениям σ;=3% и не изменяется по месяцам. Таким образом, единственной проблемой является выбор значений параметра μ; для каждого месяца. Как следует из допущений, для месяцев 1 и 2 имеем выражения:

среднее для месяца 1= (исходное среднее)*(1 + dzc %/100),

среднее для месяца 2 = (среднее для месяца 1)* (1 + dzc %/100).

Или:

среднее для месяца 2 = (исходное среднее)*(1 + dzc %/100)².

Таким образом:

среднее для месяца n = (исходное среднее)*(1 + dzc %/100) ⁿ.

Формула для индивиду­альной месячной потребности в медицинских услугах (для месяца с номером n) в Excel, может иметь вид: = НОРМОБР(СЛЧИС(), zc *(1 + dzc %/100) ⁿ,0,03).

Функция Excel НОРМОБР(вероятность; среднее; стандартное_откл) возвращает обратное нормальное распределение для указанного среднего и стандартного отклонения.

Созданную стохастическую модель можно использовать для имитационного моделирования, заключающегося в проведении численных экспериментов с моделью.

Получим совокупность (»300) возможных значений выходной переменной (выборки), анализируя которую, мы можем определить характеристики этой слу­чайной величины, сохранив при этом полученные результаты на специальном рабочем листе ЭТ, который мы назовем "Имитация".

Т.к. нужно выполнить 300 пересчетов модели (численных экспериментов), поместить последовательность номеров 1, 2, 3,...,300 в первый столбец ЭТ, начи­ная с ячейки A3.

Перенесем значение суммар­ных доплат компании из ячейки, допустим, G20 модели, находящейся на листе 1, в ячейку B3 листа "Имитация". Для этого введем в ячей­ку ВЗ листа "Имитация" следующую формулу: = Лист1!G20.

Таким образом в колонке В будут формироваться значения доплат компании при имитации. Чтобы заполнить колонку В можно воспользо­ваться режимом Таблица из меню ДАННЫЕ следующим образом.

­ Выделить блок АЗ:В302.

­ Выбрать режим Таблица данных в меню ДАННЫЕ/Анализ «что если».

В открывшемся диалоговом окне в поле «Подставлять значения по строкам» в указать ячейку А1. Кнопка ОК.

Для сохранения от изменений набор значений в столбце В сле­дует заменить содержащиеся в его ячейках формулы их значениями следующим образом. Реализовать это можно указав пункт контекстного меню Специальная вставка.

После выполнения команды получим список 200-500 возможных значе­ний случайной переменной "Доплаты компании". Заметим, что зна­чения выбираются случайным образом из большого числа возмож­ных значений. Для полученной таблицы можно вычислить среднее арифметическое значение, стандартное отклонение распределения, минимальное и максимальное значения доплат компании.

EXCEL включает возможности статистической обработки, нахо­дящиеся в меню Данные/Анализ данных/Описательная статистика. Выполнить статистическую обработку данных (среднее арифметическое значение, стандартное отклонение распределения, минимальное и максимальное значения) можно и с помощью статистических функций.

Числовые характеристики выборки, например, такие как математическое ожидание (среднее арифметическое), называются точечными, т.к. они определяются одним числом. Однако при небольших размерах выборки точечная оценка может значительно отличаться от оцениваемого параметра. Поэтому в практике используется интервальная оценка (два числа – начало и конец интервала) устанавливающая точность и надежность оценок. Такие интервалы называются доверительными. Т.е. доверительные интервалы для среднего задают область вокруг среднего, в которой с заданным уровнем доверия содержится "истинное" среднее (x = x_сред ± Δx), где Δx = t*S_xсред.

Среднеквадратичная ошибка среднего арифметического 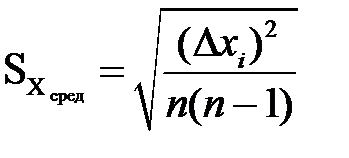.Коэффициент Стьюдента t определяется по таблицам для заданной надежности Р (обычно – 0,9; 0,95; 0,99) и размера выборки n. Например, величина t(Р, n) - t(0,95, 20)=2,093; t(0,95, 40)=2,021; t(0,95, 120)=1,98; t(0,95, ∞)=1,96.