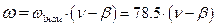Расчет статических характеристик электропривода системы ПЧ-Д с АИН
По данным крана ККТС-20 для расчета принимаем асинхронный электродвигатель с короткозамкнутым ротором типа 4А225М8У3 со следующими паспортными данными: Рном = 30 кВт U1ном = 380/660 В nн = 735 об/мин λ = Мкр/Мном = 2.1 рп = 4 Jдв = 0.74 кг∙м2 ηном = 90.5% cosφном = 0.81
1. Номинальный ток фазы статора
где U1ном = 380 В – фазное напряжение статора. Рном – номинальная мощность электродвигателя; сos φном – номинальный коэффициент мощности; ηном – номинальный КПД.
2. Линейный номинальный ток статора
3. Из условия Iпч = 71 А > Iлном = 62.1 А.
4. Активное сопротивление фазы статора
где
5. Угловая скорость магнитного поля статора
6. Номинальный и критический моменты двигателя
где Мкр – критический момент двигателя.
7. Индуктивное сопротивление короткого замыкания
8. Индуктивные сопротивление статора и приведенное ротора
9. Приведенное активное сопротивление фазы ротора
11. Номинальный приведенный ток ротора
12. Номинальный коэффициент мощности роторной цепи
Тогда
13. Номинальный ток намагничивающего контура
14. Номинальная ЭДС фазы статора
15. Индуктивное сопротивление намагничивающей цепи
16. Коэффициенты рассеяния статора и ротора
17. Общий коэффициент рассеяния
18. Определение величин b, c, d, e Введем обозначения
При этом
19. Определим коэффициенты, необходимые для расчета электромеханических и механических характеристик
Где β; – абсолютное скольжение двигателя; ν; = f1 / f1ном – относительная частота тока статора; f1ном – номинальная частота питающей сети;
20. Критическое скольжение при ν;<1.0 определяем по формуле
21. Критическое скольжение при ν;≥1.0. Причем в диапазоне ν;=1.4÷1.0 эта величина практически не меняется, поэтому в примере используем ν;=1.4.
22. Для получения семейства характеристик задаемся относительной частотой ν;: 1.4; 1.2; 1.0; 0.8; 0.6; 0.4; 0.2. Для этих относительных частот задаемся параметром абсолютного скольжения β от 0 до 1.0, включая величины номинального и критических скольжений. Расчет коэффициентов сводим в таблицу 1, используя данные, полученные в п.19.
Таблица 2.1. Расчет коэффициентов А(n), В(n), С(n).
23. Уравнения электромеханической и механической характеристик для основного закона частотного регулирования при ν;<1.0
При ν;≥1.0
Угловая скорость вала двигателя вычисляется по следующей формуле:
Используя данные таблицы 2.1,осуществляется расчет электромеханических и механических характеристик, представленный в таблице 2.2.
Таблица 2.2. Расчет статических характеристик двигателя для основного закона частотного регулирования.
Графический вид электромеханических и механических характеристик, построенных по данным таблицы 2.2., представлен на рис.2.2 и 2.3.
|

 А.
А.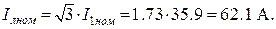
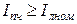 выбираем преобразователь частоты марки Mitsubishi серии FR-A540EC типа 37к, для которого:
выбираем преобразователь частоты марки Mitsubishi серии FR-A540EC типа 37к, для которого: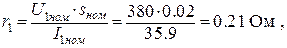
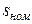 =
= 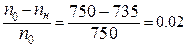

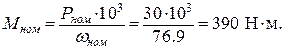

 с-1 – номинальная угловая скорость вала двигателя;
с-1 – номинальная угловая скорость вала двигателя;
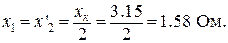
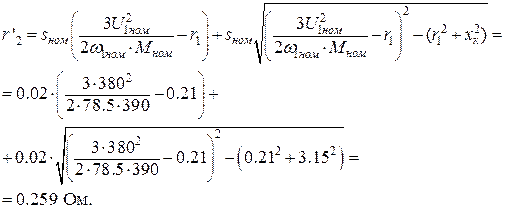

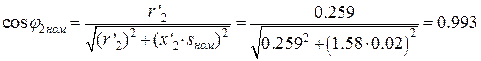 .
.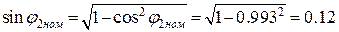 .
.
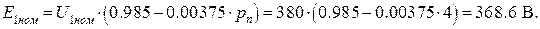
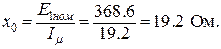




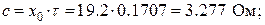
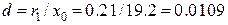 ;
;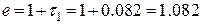 .
.

 ;
; .
.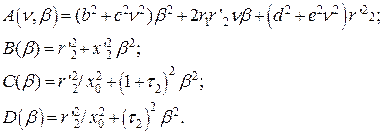
 .
. .
.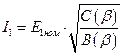 ;
; 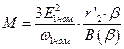 .
. ;
;  .
.