Проектирование систем типа МамданиЛабораторная работа №5 Построение нечетких систем в диалоговом режиме с помощью модуля Fuzzy
Цель работы: приобретение навыков создания нечетких систем в режиме диалога с помощью модуля Fuzzy ПП MatLab
Общие положения
Модуль fuzzy позволяет строит нечеткие системы двух типов - Мамдани и Сугэно. В системах типа Мамдани база знаний состоит из правил вида “Если x1=низкий и x2=средний, то y=высокий”. В системах типа Сугэно база знаний состоит из правил вида “Если x1=низкий и x2=средний, то y=a0+a1x1+a2x2";. Таким образом, основное отличие между системами Мамдани и Сугэно заключается в разных способах задания значений выходной переменной в правилах, образующих базу знаний. В системах типа Мамдани значения выходной переменной задаются нечеткими термами, в системах типа Сугэно - как линейная комбинация входных переменных.
Проектирование систем типа Мамдани
Основные этапы проектирования систем типа Мамдани рассмотрим на примере создания системы нечеткого логического вывода, моделирующей зависимость
Проектирование системы нечеткого логического вывода будем проводить на основе графического изображения указанной зависимости. Для построения трехмерного изображения функции
%Построение графика функции y=x1^2*sin(x2-1) %в области x1є[-7,3] и x2є[-4.4,1.7] n=15; x1=-7:10/(n-1):3; x2=-4.4:6.1/(n-1):1.7; y=zeros(n,n); for j=1:n y(j,:)=x1.^2*sin(x2(j)-1); end surf(x1,x2,y) xlabel('x1') ylabel('x2') zlabel('y') title('Target');
|
, 
.
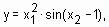в области будем использовать следующую программу:
