Проектирование систем типа Сугэно

Рассмотрим основные этапы проектирования систем типа Сугэно на примере создания системы нечеткого логического вывода, моделирующей зависимость , (рис. 3.1). Моделирование этой зависимости будем осуществлять с помощью следующей базы знаний:

Если x1=Средний, то y=0;

Если x1=Высокий и x2=Высокий, то y=2x1+2x2+1;

Если x1=Высокий и x2=Низкий, то y=4x1-x2;

Если x1=Низкий и x2=Средний, то y=8x1+2x2+8;

Если x1=Низкий и x2=Низкий, то y=50;

Если x1=Низкий и x2=Высокий, то y=50.

Проектирование системы нечеткого логического вывода типа Сугэно состоит в выполнении следующей последовательности шагов.

Шаг 1. Для загрузки основного fis-редактора напечатаем слова fuzzy в командной строке. После этого откроется нового графическое окно.

Шаг 2. Выберем тип системы. Для этого в меню File выбираем в подменю New fis… команду Sugeno.

Шаг 3. Добавим вторую входную переменную. Для этого в меню Edit выбираем команду Add input.

Шаг 4. Переименуем первую входную переменную. Для этого сделаем один щелчок левой кнопкой мыши на блоке input1, введем новое обозначение x1 в поле редактирования имени текущей переменной и нажмем <Enter>.

Шаг 5. Переименуем вторую входную переменную. Для этого сделаем один щелчок левой кнопкой мыши на блоке input2, введем новое обозначение x2 в поле редактирования имени текущей переменной и нажмем <Enter>.

Шаг 6. Переименуем выходную переменную. Для этого сделаем один щелчок левой кнопкой мыши на блоке output1, введем новое обозначение y в поле редактирования имени текущей переменной и нажмем <Enter>.

Шаг 7. Зададим имя системы. Для этого в меню File выбираем в подменю Export команду To disk и введем имя файла, например, FirstSugeno.

Шаг 8. Перейдем в редактор функций принадлежности. Для этого сделаем двойной щелчок левой кнопкой мыши на блоке x1.

Шаг 9. Зададим диапазон изменения переменной x1. Для этого напечатаем -7 3 в поле Range (см. рис. 10) и нажмем <Enter>.

 

 

Рис 10. Функции принадлежности переменной x1

 

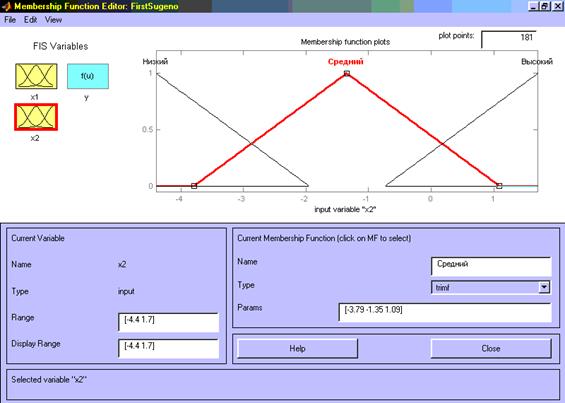
Шаг 10. Зададим функции принадлежности переменной x1. Для лингвистической оценки этой переменной будем использовать, 3 терма с треугольными функциями принадлежности, которые установлены по умолчанию. Зададим наименования термов переменной x1. Для этого делаем один щелчок левой кнопкой мыши по графику первой функции принадлежности (см. рис. 3.9). Затем напечатаем наименование терма Низкий в поле Name. Затем делаем один щелчок левой кнопкой мыши по графику второй функции принадлежности и вводим наименование терма Средний в поле Name. Еще раз делаем один щелчок левой кнопкой мыши по графику третьей функции принадлежности и вводим наименование терма Высокий в поле Name и нажмем <Enter>. В результате получим графическое окно, изображенное на рис. 3.9.

Шаг 11. Зададим функции принадлежности переменной x2. Для лингвистической оценки этой переменной будем использовать 3 терма с треугольными функциями принадлежности, которые установлены по умолчанию. Для этого активизируем переменную x2 с помощью щелчка левой кнопки мыши на блоке x2. Зададим диапазон изменения переменной x2. Для этого напечатаем -4.4 1.7 в поле Range (см. рис. 11) и нажмем <Enter>. По аналогии с предыдущим шагомзададим следующие наименования термов переменной x2: Низкий, Средний, Высокий. В результате получим графическое окно, изображенное на рис 11.

 

 

Рис 11. Функции принадлежности переменной x2

 

Шаг 12. Зададим линейные зависимости между входами и выходом, приведенные в базе знаний. Для этого активизируем переменную y с помощью щелчка левой кнопки мыши на блоке y. В правом верхнем угле появилось обозначение трех функций принадлежности, каждая из которых соответствует одной линейной зависимости между входами и выходам. В базе знаний, приведенной в начале подраздела 3.2 указаны 5 различных зависимостей: y=50; y=4x1-x2; y=2x1+2x2+1; y=8x1+2x2+8; y=0. Поэтому добавим еще две зависимости путем выбора команды Add Mfs… меню Edit. В появившимся диалоговом окне в поле Number of MFs выбираем 2 и нажимаем кнопку OK.

Шаг 13. Зададим наименования и параметры линейных зависимостей. Для этого делаем один щелчок левой кнопкой мыши по наименованию первой зависимости mf1. Затем печатаем наименование зависимости, например 50, в поле Name, и устанавливаем тип зависимости – константа путем выбора опции Сonstant в меню Type. После этого вводим значение параметра – 50 в поле Params.

Аналогично для второй зависимости mf2 введем наименование зависимости, например 8+8x1+2x2. Затем укажем линейный тип зависимости путем выбора опции Linear в меню Type и введем параметры зависимости 8 2 8 в поле Params. Для линейной зависимости порядок параметров следующий: первый параметр – коэффициент при первой переменной, второй – при второй и т.д., и последний параметр – свободный член зависимости.

Аналогично для третьей зависимости mf3 введем наименование зависимости, например 1+2x1+2x2, укажем линейный тип зависимости и введем параметры зависимости 2 2 1.

Для четвертой зависимости mf4 введем наименование зависимости, например 4x1-x2, укажем линейный тип зависимости и введем параметры зависимости 4 -1 0.

Для пятой зависимости mf5 введем наименование зависимости, например 0, укажем тип зависимости - константа и введем параметр зависимости 0.

В результате получим графическое окно, изображенное на рис. 12.

 

 

Рис 12. Окно линейных зависимостей “входы-выход”

 

Шаг 14. Перейдем в редактор базы знаний RuleEditor. Для этого выберем в меню Edit команду Edit rules.... и введем правила базы знаний. Для ввода правила необходимо выбрать соответствующую комбинацию термов и зависимостей и нажать кнопку Add rule. На рис. 13 изображено окно редактора базы знаний после ввода всех шести правил.

 

 

Рис 13. Нечеткая база знаний для системы типа Сугэно

 

На рис. 14 приведено окно визуализации нечеткого логического вывода. Это окно активизируется командой View rules... меню View. В поле Input указываются значения входных переменных, для которых выполняется логический вывод. Как видно из этого рисунка значение выходной переменной рассчитывается как среднее взвешенное значение результатов вывода по каждому правилу.

 

 

Рис. 14 Визуализация нечеткого логического вывода для системы типа Сугэно

 

На рис. 15 приведена поверхность “входы-выход”, соответствующая синтезированной нечеткой системе. Для вывода этого окна необходимо использовать команду View surface... меню View. Сравнивая поверхности на рис. 3.1, рис. 3.8 и на рис. 3.14 можно сделать вывод, что нечеткие правила достаточно хорошо описывают сложную нелинейную зависимость. При этом, модель типа Сугэно более точная. Преимущество моделей типа Мамдани состоит в том, что правила базы знаний являются прозрачными и интуитивно понятными, тогда как для моделей типа Сугэно не всегда ясно какие линейные зависимости “входы-выход” необходимо использовать.

 

 

Рис 15. Поверхность “входы-выход” для системы типа Сугэно