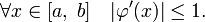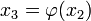Метод простой итерацииВ основе метода заложено понятие сжимающего отображения. Определим терминологию: Говорят, что функция Тогда основная теорема будет выглядеть так:
Поясним смысл параметра
Отсюда следует, что ......... и так далее, пока
Выводы: в данной работе я реализовал метод половинного деления в среде Паскаль и проверил его работу на примере решения конкретного уравнения. Функциональные уравнения делятся на: алгебраические, а также трансцендентные. Здесь я решал алгебраическое уравнение. После алгебраических изменений с любого алгебраического уравнения можно получить уравнение в канонической форме, а затем, в большенстве случаев, этот этап проводят графически, однако в Паскале построить график практически не возможно, на этом этапе у меня и возникли трудности… к счастью построение графика не есть обязательным, что дало мне возможность обойти его стороной. Однако в Маткаде я таки построили график. Сложности встречаются когда не только на первом этапе – при выделении промежутков, которые вмещают в себе корни уравнений, а и при следущем решении уравнения расчеты проводят не по основной функции, а по приближенной к ней: F2(x). В нашем случае расчеты проводились не по приближенной функции. Я показал как правильно отеделять корни методом половинного деления, методом хорд и методом простой итерации.
|
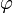осуществляет сжимающее отображение на 
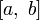, если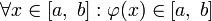
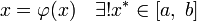— корень;
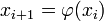сходится к этому корню;
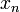справедливо 
.
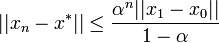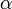. Согласно теореме Лагранжа имеем:
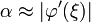. Таким образом, для сходимости метода достаточно, чтобы 
