Задача 1. Тема: Решение задач линейного программирования и анализ чувствительности с помощью MS Excel.
Лабораторная работа №1 Тема: Решение задач линейного программирования и анализ чувствительности с помощью MS Excel. Цель: Изучить возможности надстройки Поиск решения пакета MS Excel для решения однокритериальных задач теории принятия решений. Порядок выполнения работы: 1. Изучение теории и примера. 2. Построение математической модели проблемы в виде задачи линейного программирования. 3. Решение задачи с использованием надстройки Поиск решения пакета MS Excel. 4. Анализ чувствительности решения с использованием сценариев. 5. Составление отчёта по лабораторной работе, в котором представляется: · формулировка индивидуального задания; · математическая модель и пояснение к её построению; · снимок экрана монитора, содержащий табличную модель задачи, снимки отчетов по результатам, устойчивости и пределам, а также снимок отчета по сценариям с содержательными пояснениями к ним; · выводы по лабораторной работе.
Теория
Процесс принятия управленческого решения можно представить как последовательность выполнения следующих действий (этапов выработки решения). I. Анализ ситуации и формализация исходной проблемы. На этом этапе надо просто четко сформулировать проблему, понять и сформулировать цели, которые хочется достичь в виде решения проблемы. Другими словами, надо поставить проблему, четко определить цели, возможные решения и факторы, влияющие на решение проблемы. Часто результат этого этапа представляют в виде формальной модели проблемы (пока записанной обычным языком), где были бы собраны воедино цели, решения и факторы и где бы присутствовала основа для формализации отношений между ними. II. Построение математической модели, т. е. перевод формальной модели, построенной на предыдущем этапе, на язык математических отношений. III. Анализ математической модели и получение математического решения проблемы. На этом этапе анализируется построенная математическая модель, проверяется адекватность модели и находится решение математической задачи, вытекающей из этой модели. Если для решения математической задачи используется вычислительная техника, то предварительно строится также компьютерная модель задачи. Обычно этот этап наиболее простой из всех этапов процесса принятия решения, поскольку здесь, как правило, используются известные и апробированные алгоритмы решения математических задач. IV. Анализ математического решения проблемы и формирование управленческого решения. На этом этапе анализируется полученное математическое решение (выполняется так называемый анализ чувствительности), и затем на основе этого математического решения формируется управленческое решение. После выполнения этих этапов следует этап реализации принятого решения.
I. Рассмотрим первый этап процесса принятия решения: анализ проблемы и формализация исходной проблемы. Этот этап можно рассматривать как первую стадию перехода от реального мира к компьютерному представлению проблемы. На данном этапе надо четко сформулировать свою проблему, понять и сформулировать цели, которые хочется достичь в виде решения проблемы. Другими словами, надо четко поставить проблему. Поэтому на данном этапе на простом русском языке надо ♦ сформулировать проблему, по возможности максимально четко; ♦ сформулировать цели, которые должны быть достигнуты в результате реализации найденного решения; ♦ указать, что считать решением проблемы (решение должно гарантировать достижение целей); ♦ выявить и описать возможности достижения целей; ♦ выявить и описать факторы, от которых может зависеть решение проблемы; ♦ выявить и описать ограничения, препятствующие достижению целей; ♦ описать возможные альтернативные способы решения проблемы. Эти пункты и составляют формальную модель проблемы. Таким образом, формальная модель — это просто четкое описание вашей проблемы, в котором необходимо выделить перечисленные пункты.
Пусть некий лакокрасочный завод «Олимп», в связи с изменившейся конъюнктурой рынка хочет разработать новый производственный план для выпуска краски типов А и Б, не трогая пока производство другой продукции. Допустим, что «Олимп» имеет месячный цикл производства. Таким образом, нужно определить, сколько в месяц следует производить краски типа А и сколько — типа Б. Ответ вроде бы простой: чем больше, тем лучше, конечно, с учетом производственных возможностей. Итак, вот первая цель — увеличить до максимума производство как продукции А, так и продукции Б. Допустим, производственные мощности позволяют выпускать в месяц суммарно 500 т краски всех типов. Вот появилось первое ограничение — общее количество краски типов А и Б не должно превышать 500 т. Как видно, первую цель достичь можно, однако проблема остается плохо поставленной, поскольку дает неоднозначное решение. Поэтому вспомним, что всякое производство должно приносить прибыль. Теперь можно сформулировать вторую цель — производственный план должен приносить максимальную прибыль. Пусть одна тонна краски А приносит в среднем 2000 руб. прибыли, а одна тонна краски Б — 2500 руб. Здесь величины удельной прибыли (т.е. прибыли на одну тонну краски) являются факторами, которые влияют на конечную цель. На этом шаге мы сделали огромное упрощение реальной ситуации, т. к. удельная прибыль любого производимого изделия зависит от многих факторов (конъюнктуры рынка, стоимости исходных материалов, себестоимости производства, уровня рентабельности и т. д.) и не является величиной постоянной даже на протяжении относительно небольшого временного промежутка. Тем более сложно предсказать и трудоемко подсчитать ее значение на будущий более-менее продолжительный период времени. Можно только оценить будущую удельную прибыль, да и то с определенной степенью точности. Пусть в нашем примере получены оценки будущей удельной прибыли производства краски типа А: от 1500 до 2300 руб., а краски типа Б: от 2100 до 3000 руб. Приведенные выше величины удельных прибылей 2000 и 2500 руб. являются наиболее вероятными ожидаемыми значениями. Далее именно эти величины примем за значения удельных прибылей, а возможные последствия от их неточного задания рассмотрим при проведении анализа полученного решения. Очевидно, что для достижения второй цели надо производить только краску типа Б и забыть о краске типа А. Однако отдел маркетинга требует, чтобы краски типа А производилось не менее 200 т в месяц, поскольку есть договоры на такое количество, а краску типа Б нельзя производить более 150 т, поскольку большее количество трудно реализовать. Итак, имеем еще два ограничения: произведенное количество краски А должно быть не меньше 200 т, а краски Б — не более 150 т. При таких ограничениях даже начальник производства составит план: надо производить 350 т краски А и 150 т краски Б. Этот план учитывает только ограничения по производственным мощностям и маркетинговые ограничения. Но для производства любой продукции нужны еще исходные материалы. Пусть на изготовление красок А и Б необходимо сырье трех видов согласно следующей таблице.
В этой таблице показано, сколько и какого сырья необходимо для производства одной тонны краски А и одной тонны краски Б, а также величины месячных запасов этого сырья. Очевидно, что общее количество сырья, используемого для производства краски, не должно превышать их месячные запасы. Таким образом, имеем еще три ограничения — по одному для каждого типа сырья. С учетом этих ограничений производственный план «на пальцах» уже не подсчитаешь. Здесь сделано еще одно существенное упрощение реальной ситуации — реальный процесс производства чего бы то ни было зависит не только от наличия исходных материалов, необходимых для создания конечного продукта, но и от многих других факторов: наличия достаточных производственных мощностей, наличия рабочей силы, периодичности поступления исходных материалов, качества этих материалов и т.д. Здесь эти факторы отброшены, оставлены только ограничения на сырье трех видов. При этом сделано еще одно неявное допущение, что другие компоненты, необходимые для производства краски, имеются в достаточном количестве и не влияют на объемы производства. Итак, что же мы имеем после небольшого анализа проблемы.
♦ Постановка проблемы: разработать производственный план, который максимизировал бы прибыль с учетом всех видов ограничений. ♦ Цель: максимизировать прибыль. ♦ Решение: количество тонн краски А и Б, производимых в месяц. ♦ Факторы, от которых зависит решение: значения удельной прибыли каждого типа краски, предельное число производимой краски, предельные числа производимых красок типов А и Б (маркетинговые ограничения), количества сырья (необходимых для производства одной тонны краски), значения запасов сырья (всего 14 факторов). ♦ Факторы, влияющие на прибыль: все перечисленные факторы, кроме значений количества сырья, необходимого для производства одной тонны краски. (Считаем, что на рецептуру красок мы влиять не можем.) ♦ Ограничения: на предельное общее количество производимой краски, на предельные количества производимых красок А и Б в отдельности, на предельные количества используемого сырья (всего 6 ограничений).
Мы выделили факторы, влияющие на прибыль отдельно, чтобы в дальнейшем провести анализ чувствительности решения именно по этим факторам. И еще одно замечание: при такой размытой постановке исходной проблемы можно сформулировать много разных целей. Например, можно составить производственный план, который бы минимизировал себестоимость продукции. Можно сформулировать более сложные цели (что обычно имеет место в реальных ситуациях), например, максимизировать прибыль и одновременно минимизировать использование каких-то исходных материалов, которые являются дорогими или дефицитными. При этом в зависимости от сформулированных целей могут выделяться разные факторы, влияющие на эти цели, и могут формироваться разные ограничения. В нашем примере мы ограничимся сформулированной целью максимизации прибыли.
II. Построение математической модели означает перевод формальной модели, построенной на предыдущем этапе, на четкий язык математических отношений. Математическая модель должна содержать три основных компонента. 1. Переменные, значения которых необходимо вычислить (это переменные решения из формальной модели). 2. Целевая функция — это цель, записанная математически в виде функции от переменных. Обязательно указывается, что необходимо сделать с этой функцией для решения проблемы: найти ее максимум, минимум или конкретное заданное значение. 3. Ограничения — записанные математически ограничения из формальной модели. Если определены переменные, то построение целевой функции и ограничений обычно не вызывает затруднений, поскольку на предыдущем этане и цель и ограничения уже формулировались с привязкой к переменным решения. В нашем примере обозначим через х1 и х2 переменные, которые определяют месячные объемы производства краски (в тоннах) типа А и Б соответственно. Напомним, что 1 тонна краски А приносит прибыль 2000 руб., а 1 тонна краски Б — 2500 руб. Тогда суммарная прибыль z при производстве х1 тонн краски А и х2 тонн краски Б составит
z = 2000*х1 + 2500*х2 (руб.)
Это и есть целевая функция, которую необходимо максимизировать. Теперь запишем ограничения. Первое ограничение говорит о том, что суммарный объем производства краски обоих типов не должен превышать 500 т. Это запишется так: х1 + х2 £ 500. Маркетинговые ограничения записываются просто: х1 ³ 200 и х2 £ 150. Теперь надо записать ограничения па сырье. Напомним, что сырья 1 на производство 1 т краски А расходуется 0,05 т (50 кг) и 0,1 т (100 кг) на производство 1 т краски Б. Таким образом, всего на производство x1, тонн краски А и x2 тонн краски Б потребуется 0,05*х1 + 0,1*х2 тонн сырья 1. Эта величина не должна превышать 50 т. Отсюда получаем ограничение: 0,05*х1 + 0,1*х2 £ 50. Подобным способом получаем еще два ограничения на сырье 2 и сырье 3: 0,07*x1 + 0,08*x2 £ 30 и 0,04*x1 + 0,07*x2 £ 25. Еще одно неявное ограничение состоит в том, что переменные х1 и х2 должны быть неотрицательными (если не вдаваться в мистику, то отрицательные объемы производства физически просто невозможны). Это ограничение называется условием неотрицательности переменных и записывается так: х1 ³ 0 и х2 ³ 0. Однако заметим, что условие неотрицательности для переменной х1 здесь излишне, поскольку имеем более сильное ограничение х1 ³ 200. Поэтому неравенство х1 ³ 0 исключаем из списка ограничений. Обратите особое внимание на то, что размерности всех переменных и параметров должны быть согласованы. Поэтому в нашем примере удельные расходы сырья переведены из килограммов в тонны, поскольку переменные измеряются в тоннах. Обычно ограничение записывают таким образом, чтобы в левой части неравенства находилось выражение с переменными, а в правой части неравенства — только числа. Тогда левую часть неравенства называют функцией ограничения. Окончательно математическая модель нашей проблемы запишется следующим образом:
максимизировать z = 2000*х1 + 2500*х2 при выполнении ограничений
х1 + х2 £ 500, х1 ³ 200, х2 £ 150, 0,05*х1 + 0,1*х2 £ 50, 0,07*x1 + 0,08*x2 £ 30, 0,04*x1 + 0,07*x2 £ 25, х2 ³ 0.
Любое решение (т.е. пара значений переменных х1 и х2), удовлетворяющее всем ограничениям модели, называется допустимым. В нашем примере решение х1 = 200 и х2 = 150 будет допустимым, поскольку не нарушает ни одного ограничения, включая условия неотрицательности. Чтобы убедиться в этом, надо подставить значения х1 = 200 и х2 = 150 в левые части ограничений, выполнить вычисления и проверить, что ни одно неравенство не нарушается. Значение целевой функции при этом решении будет равно z = 2000*200 + 2500*150 = 775 000 (руб.). Итак, математическая модель построена, осталось найти решение модели. Для выполнения этого дела мы привлечем программу электронных таблиц Excel, а еще точнее — надстройку Поиск решения.
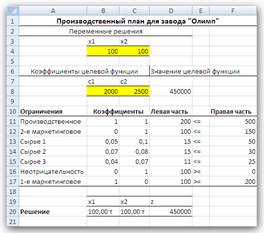
III. Прежде чем начать выполнение каких-либо вычислений в Excel, надо перевести нашу построенную математическую модель на рабочий лист Excel. Для этого следует определить, в каких ячейках будут располагаться переменные решения, записать в нужные ячейки формулы, по которым будут вычисляться целевая функция и функции ограничений (левые части ограничений), надо записать в отдельные ячейки значения правых частей ограничений. Всю эту совокупность значений и формул, записанных на рабочем листе, назовем табличной моделью. Для табличных моделей задач оптимизации не существует общепринятых канонов их построения. Вот некоторые рекомендации, которые облегчат дальнейшее применение средства Поиск решения. ♦ Значения переменных располагаются в отдельных ячейках и группируются в отдельный блок ячеек. ♦ Каждому ограничению отводится отдельная строка или столбец таблицы. Ограничения группируются в отдельный блок ячеек. ♦ Желательно, чтобы ячейки, содержащие переменные и значение целевой функции, а также все ограничения, имели заголовки. ♦ Коэффициенты целевой функции должны храниться в отдельной строке, располагаясь непосредственно под или над соответствующими переменными; формула для вычисления целевой функции должна находиться в соседней ячейке. ♦ В каждой строке ограничений за ячейками, содержащими коэффициенты данного ограничения, следует ячейка, в которую записывается вычисленное значение функции ограничения (значение левой части ограничения). За ней может следовать ячейка, в которой стоит соответствующий знак неравенства или равенства ограничения, а затем ячейка, содержащая значение правой части ограничения. Желательно, чтобы правые части ограничений были константами, а не формулами. Дополнительно можно иметь ячейку, в которой вычислена разность между значениями левой и правой частей неравенства. ♦ Условия неотрицательности переменных решения не обязательно включать в табличную модель. Как правило, они опускаются и указываются непосредственно в диалоговом окне средства Поиск решения. В результате выполнения этих рекомендаций все основные коэффициенты модели содержатся в отдельных ячейках, поэтому их легко изменять, не меняя формул модели. Благодаря группированию упрощается работа со средством Поиск решения, поскольку для указания переменных или ограничений можно использовать диапазоны ячеек, т.е. задавать переменные и ограничения группой, а не по отдельности. Наличие заголовков сделает понятной эту табличную модель не только вам, но и другим людям. Пример табличной модели для нашей задачи показан на рис. 1. Здесь значения переменных решения записаны в ячейках В4 и С4 с соответствующими заголовками в ячейках В3 и С3. Вначале значения переменных произвольные. Коэффициенты, стоящие перед переменными в формуле целевой функции, записаны в ячейки В8 и С8, а само значение целевой функции вычисляется в ячейке D8 (соответствующие заголовки записаны над этими ячейками). Ниже в диапазоне В11:С17 записаны коэффициенты функций ограничений, в диапазоне D11:D17 вычисляются значения левых частей ограничений, в диапазоне Е11:Е17 записаны знаки неравенств ограничений, а в диапазоне Fl1:F17 — значения правых частей ограничений. Наконец, внизу в строке 20 под «левым» заголовком Решение еще раз повторены значения переменных и целевой функции.
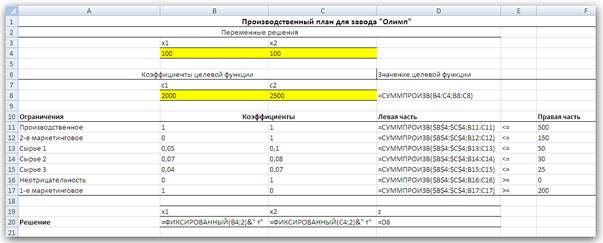
Рис. 1. Табличная модель для вычисления производственного плана Формулы, по которым выполняются все вычисления на данном рабочем листе, показаны на рис. 2. Для вычисления линейных функций подходит функция СУММПРОИЗВ(массив1;массив2), которая суммирует попарные произведения элементов двух диапазонов, заданных аргументами функции массив1 и массив2. Например, формула =СУММПРОИЗВ($В$4:$С$4;В8:С8), вычисляющая значение целевой функции в ячейке D8, эквивалентна такой формуле: =В4*В8+С4*С8. Абсолютные ссылки $В$4:$С$4 на диапазон В4:С4, содержащий значения переменных х1 и х2, сделаны для того, чтобы можно было скопировать эту формулу из ячейки D8 в ячейки D11:D17 для вычисления левых частей неравенств, где также участвуют значения переменных решения.
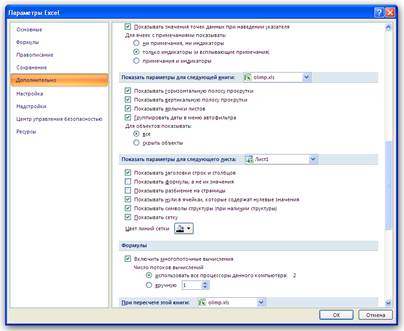
Рис. 2. Формулы табличной модели Левые части ограничений, поскольку это линейные функции, также вычисляются с помощью функции СУММПРОИЗВ. Даже если это простые ограничения типа х2 £ 150, которые здесь представляются как 0*x1 + 1*х2 £ 150 (ограничение 2 на рис. 1). Обратите внимание на то, что ограничения сгруппированы по типу неравенств — сначала идут ограничения типа <=, а затем типа >=. Конечно, порядок представления этих групп несущественен. Существенно само наличие групп однотипных ограничений, что позволит в дальнейшем задавать их в средстве Поиск решения не по отдельности, а целой группой. Знаки неравенств в диапазоне Е11:Е17 вставлены только для пояснения ограничений, средство Поиск решения их не использует. Зато средство Поиск решения использует заголовки строк, содержащих ограничения (использует в своих отчетах, как показано далее). Поэтому рекомендуется давать более содержательные заголовки, даже чем те, что показаны на рис. 1 в ячейках А11:А17. Например, такие: Ограничение на объем производства, Маркетинговое ограничение или Ограничение, не знаю, откуда оно взялось. С другой стороны, заголовки не являются обязательным элементом табличной модели — средство Поиск решения прекрасно вычислит результат и без них. Заголовки полезны для документирования модели. Если вы не знаете, как отобразить на рабочем листе Excel формулы, а не значения (как на рис. 2), то это делается так. Надо выполнить команду Сервис->Параметры и в открывшемся диалоговом окне Параметры на вкладке Вид установить флажок формулы. Отображение формул может оказаться полезным, полезно при отладке модели. В Excel 2007 и выше отображение формул осуществляется через меню Параметры Excel ->Дополнительно, выбирая для данного листа Показывать формулы, а не их значения
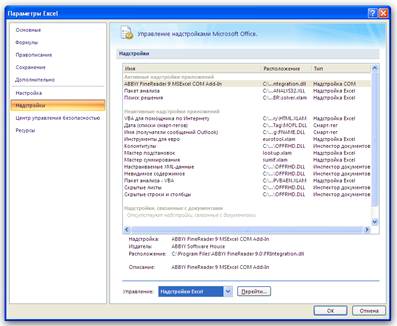
Теперь, когда табличная модель построена и проверена, пришло время ее решить. Для этого используем надстройку Excel Поиск решения. Если в меню Сервис вы не находите одноименной команды, то это означает, что данная надстройка не подключена к Excel. Для ее подключения выполните команду Сервис->Надстройки и в открывшемся диалоговом окне Надстройки в списке Доступные надстройки установите флажок Поиск решения. Для Excel 2007 и выше Поиск решения находится во вкладке Данные->Анализ. Подключение осуществляется через меню Параметры Excel ->Надстройки. Выбираем в списке Надстройки Excel и нажимаем кнопку Перейти…
Покажем общую схему применения средства Поиск решения для решения задач линейной оптимизации. Сначала надо познакомиться с терминологией, относящейся к средству Поиск решения, т.е. надо знать, как там называют переменные решения, целевую функцию и ограничения. Так вот, ♦ переменные решения, точнее, ячейки, содержащие значения этих переменных, называются изменяемыми ячейками, ♦ ячейка, содержащая значение целевой функции, называется целевой ячейкой, ♦ ограничения так и будут называться ограничениями.
Схема применения средства Поиск решения выглядит так: 1. Пусть на рабочем листе Excel уже создана табличная модель задачи линейной оптимизации. 2. После проверки и отладки модели переходим к этапу оптимизации, выбрав команду Поиск решения в меню Сервис. 3. В открывшемся диалоговом окне Поиск решения укажите данные, необходимые для поиска оптимального решения (рис. 3).
Рис. 3. Задание параметров для поиска решения • В поле Установить целевую ячейку вводится адрес ячейки, содержащей значение целевой функции. Для нашей модели в это поле следует ввести D8, но лучше щелкнуть указателем мыши на этой ячейке, чтобы ввести ее адрес автоматически. • Параметры области Равной диалогового окна Поиск решения позволяют задать тип оптимизации. В данном случае необходимо максимизировать значение целевой функции. Для этого нужно щелкнуть на переключателе максимальному значению. • Поле Изменяя ячейки позволяет указать ячейки, в которых содержатся переменные модели; в данном случае это диапазон В4:С4. 4. Далее необходимо задать ограничения. Щелчок на кнопке Добавить открывает диалоговое окно Добавление ограничения, показанное на рис. 4, • В нашем примере в поле Ссылка на ячейку вводим или указываем на рабочем листе ссылку на диапазон D11:D15, в соседнем поле оставляем знак неравенства <=, а в поле Ограничение вводим или указываем на рабочем листе ссылку на диапазон F11:F15. • Щелкаем на кнопке Добавить и вводим вторую группу ограничений: в поле Ссылка на ячейку вводим D16:D17, в соседнем раскрывающемся списке выбираем знак неравенства >=, а в поле Ограничение вводим F16:F17. Затем щелкаем на кнопке ОК и возвращаемся в диалоговое окно Поиск решения.
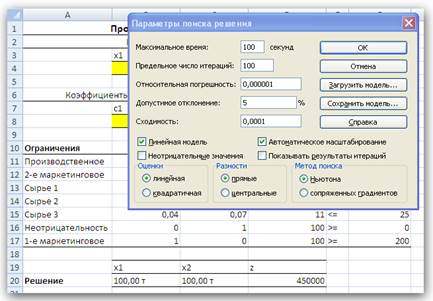
Рис. 4. Задание ограничений 5. После задания ограничений при необходимости в диалоговом окне Параметры поиска решения, которое открывается после щелчка на кнопке Параметры диалогового окна Поиск решения, следует задать дополнительные условия для поиска решения. • Параметры Максимальное время, Предельное число итераций, Относительная погрешность, Допустимое отклонение и Сходимость можно оставить без изменений, тем более что параметр Допустимое отклонение имеет отношение к целочисленным моделям, а параметр Сходимость — к нелинейным моделям. • В данном примере, поскольку мы работаем с линейной моделью, надо установить флажок Линейная модель (рис. 5). • Если в модели условия неотрицательности налагаются на все переменные, следует установить флажок Неотрицательные значения. В нашем примере условие неотрицательности налагается только на переменную x2 поэтому этот флажок мы не устанавливаем. • Флажок Автоматическое масштабирование рекомендуем устанавливать всегда. • Если хотите проследить каждую итерацию процесса вычисления, установите флажок Показывать результаты итераций. Если хотите сразу получить результат вычислений без подглядывания в вычислительную кухню, не устанавливайте этот флажок. • Переключатели, расположенные в областях Оценки, Разности, Метод поиска, предназначены для нелинейных моделей. Поэтому сейчас мы их оставляем без внимания. • Щелчок на кнопке ОК возвращает в диалоговое окно Поиск решения. 6. После задания необходимых данных (указания ячейки, содержащей формулу для вычисления целевой функции, ячеек, в которых находятся переменные, и задания ограничений) щелкните на кнопке Выполнить. 7. Средство Поиск решения выполняет оптимизацию. В процессе вычислений в строке состояния отображаются число итераций и значения целевой функции при переборе множества допустимых решений задачи. Эта информация позволяет следить, как продвигается процесс оптимизации больших моделей, где он может длиться достаточно долго. 8. После окончания работы Поиск решения выведет на экран диалоговое окно Результаты поиска решения (рис. 6), в котором можно указать, обновить ли исходную модель (т.е. занести ли в ячейки значения оптимального решения) и создавать ли отчет.
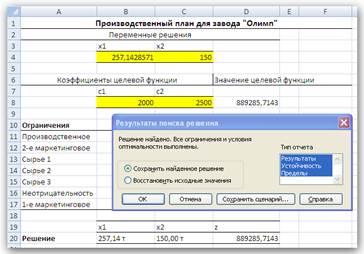
Рис. 5. Диалоговое окно Параметры поиска решения Диалоговое окно Результаты поиска решения сообщает о завершении поиска (см. рис. 6). Если оптимальное решение найдено, в диалоговом окне Результаты поиска решения должно отобразиться сообщение Решение найдено. Все ограничения и условия оптимальности выполнены. Если получено такое сообщение, можно или сохранить найденное решение, выбрав соответствующий параметр, или отбросить его, выбрав параметр Восстановить исходные значения. В результате ячейкам переменных будут возвращены значения, которые в них находились до запуска программы Поиск решения. Существует возможность также получить три типа отчетов о решении. Каждый отчет выводится на новый лист рабочей книги.
Рис. 6. Успешное завершение решения задачи оптимизации В нашем примере решение найдено, оно показано на рис. 6: надо производить 257,14 т краски А и 150 т краски Б, при этом будет получена прибыль в размере 889 285,17 руб. В диалоговом окне Результаты поиска решения мы также указали, что надо создать отчеты.
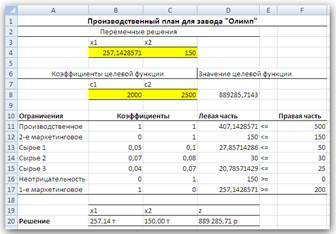
IV. Теперь покажем, что делать дальше с полученным «компьютерным» решением, и как на его основе найти «настоящее» решение проблемы. Итак, решение математической модели получено. Ну и что с ним дальше делать — бегом бежать внедрять в жизнь? Нет, бежать пока рано. Надо вспомнить, что мы получили решение только для модели реальной проблемы, а не решение самой проблемы. В процессе построения модели были сделаны различные допущения, упрощающие реальную ситуацию, в результате чего мы смогли ее формализовать. Зависимости, зафиксированные в модели, только приближенно отображают реальные зависимости между факторами и переменными решения и целью. Наши знания факторов, влияющих на цель, зияют пробелами — значения многих параметров модели мы знаем только приближенно. Ну, а если реальные значения параметров хотя бы немного отличаются от тех, которые заложены в модели, то насколько может измениться решение и изменится ли вообще? На эти и подобные вопросы должен дать ответы анализ полученного решения. На «научном» языке этот анализ называется анализом чувствительности решения. Он проводится после получения оптимального решения математической модели и дает важную информацию, которую можно и нужно использовать при принятии решения в реальной ситуации. Анализ чувствительности должен дать ответы на следующие вопросы. ♦ В каких пределах могут изменяться параметры модели так, чтобы сохранилось полученное решение? ♦ Какие ограничения связанные (т.е. лимитируют (сдерживают) целевую функцию), а какие ограничения не влияют на решение? ♦ Если изменить значения правых частей связанных ограничений, то насколько может измениться значение целевой функции? ♦ Если значение какой-то переменной решения равно нулю, то при каких условиях она может принять положительное значение? (Вопрос весьма актуален для моделей производства.) Средство Поиск решения может генерировать три вида отчетов: отчет по результатам, отчет по устойчивости и отчет по пределам. Все перечисленные виды отчетов и именно в той форме, которая показана ниже на рис. 8—10, Поиск решения создает только для линейных моделей. Для целочисленных моделей недоступны отчеты по устойчивости и по пределам, а для нелинейных моделей отчет по устойчивости имеет другой вид. Рассмотрим применение отчетов для выполнения анализа чувствительности линейных моделей. На рис. 7 показан рабочий лист Excel с найденным решением математической модели, а на рис. 8—10 — отчеты, сгенерированные средством Поиск решения.
Рис. 7. Решение линейной модели для завода «Олимп»
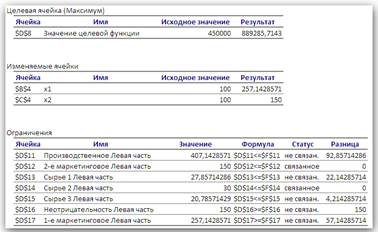
Рис. 8. Отчет по результатам Отчет по результатам полезен для анализа чувствительности только тем, что там явно указано, какие ограничения связанные и какие несвязанные. Эти данные приведены в отчете в таблице Ограничения в столбце Статус. В столбце Разница той же таблицы показаны значения разностей между левыми и правыми частями ограничений.
Рис. 9. Отчет по устойчивости Более существенен для анализа чувствительности отчет по устойчивости. В таблице Изменяемые ячейки этого отчета приведена информация о значениях изменяемых ячеек: ♦ адреса изменяемых ячеек; ♦ их имена (созданные заранее или составленные из заголовков строк и столбцов, на пересечении которых находятся изменяемые ячейки); если имен нет, то это поле остается пустым; ♦ значения переменных в этих ячейках, найденные средством Поиск решения; ♦ нормированная стоимость — это неудачный перевод термина «reduced cost», который можно перевести как «цена, которая уменьшает целевую функцию». Она показывает, как изменится оптимальное значение целевой функции при выпуске продукции, которой нет в оптимальном плане. В нашем случае оптимальный план предполагает выпуск обоих видов красок, поэтому их нормированная стоимость равна нулю. Если бы оптимальное значение какой-либо из неизвестных было равно нулю (xi = 0), а нормированная стоимость равнялась бы, например, –3, то принудительный выпуск 2-х единиц этой переменной xi (т. е. добавление нового ограничения xi ≥ 2) привел бы к изменению (уменьшению) целевой функции на 2*(–3) = –6 единиц. Отметим, что из равенства нулю оптимального значения неизвестной не следует автоматически, что ее нормированная стоимость будет отлична от нуля; ♦ целевой коэффициент — коэффициент, стоящий при данной изменяемой переменной в формуле целевой функции; ♦ значения в столбцах Допустимое увеличение и Допустимое уменьшение показывают, в каких пределах может изменяться целевой коэффициент при условии, что найденные значения переменных останутся неизменными. В таблице Ограничения приведена информация об ограничениях: ♦ адреса ячеек, на значения которых наложены ограничения; ♦ их имена (созданные заранее или составленные из заголовков строк и столбцов, на пересечении которых находятся изменяемые ячейки); если имен нет, то это поле остается пустым; ♦ значения в этих ячейках, найденные средством Поиск решения; ♦ теневая цена показывает, насколько изменится значение целевой функции, если на единицу изменится значение правой части данного ограничения; теневая цена отлична от нуля только тогда, когда данное ограничение в оптимальном решении является связанным (и решение не вырождено); ♦ значения правых частей ограничений; ♦ значения в столбцах Допустимое увеличение и Допустимое уменьшение показывают пределы изменения правой части ограничения, в которых действует приведенное значение теневой цены данного ограничения[1]. Наиболее важными данными для анализа чувствительности в этом отчете являются нормированные стоимости и теневые цены, применение которых рассмотрим ниже. Важно отметить, что значения теневых цен подсчитаны в предположении, что изменяется значение правой части только одного ограничения при условии постоянства всех остальных параметров модели. В отчете по пределам показано, в каких пределах с учетом всех ограничений могут изменяться переменные (значения в столбцах Верхний предел и Нижний предел) и какие при этом значения будет принимать целевая функция (значения в столбцах Целевой результат). Отметим, что если на значения переменной не налагаются явные ограничения, задающие ее верхнюю (или нижнюю) границу, то в столбцах Верхний предел и Целевой результат (или Нижний предел и Целевой результат) для этой переменной будут стоять значения ошибки #Н/Д.
Рис. 10. Отчет по пределам Начнем анализ чувствительности для нашего примера. Во-первых, заметим, что переменные решения нулевые значения не принимают, и это облегчает нашу жизнь. Рассмотрим ограничения. Первое ограничение, задающее предельный объем производства, лимитирующим (связанным) не является. Отсюда следует простой вывод, что такой производственный план мощности завода задействует не в полной мере. Это большой «минус» данного плана. Посмотрим, что сдерживает объемы производства. Лимитирующими являются второе маркетинговое ограничение и ограничение по сырью 2 (на это указывает отчет по результатам и ненулевые значения теневых цен для этих ограничений в отчете по устойчивости). Влиять на маркетинговое ограничение трудно, поскольку против отдела маркетинга просто так не попрешь, для этого нужны веские обоснования, а их, конечно, нет. Да это и не имеет особого смысла — чтобы полностью загрузить мощности производства, надо запланировать еще почти 93 тонны краски, а на такое увеличение производства краски типа Б «добро» никто не даст, так как даже объем в 150 тонн трудно продать. Другое лимитирующее ограничение определяется наличием на складе запаса сырья 2. Разберемся с этим параметром. Взглянем на теневую цену этого ограничения, она равна 28 571,43. Это означает, что изменение на одну единицу величины правой части данного ограничения (т.е. изменение величины запаса сырья 2 на 1 тонну) приведет к изменению на 28 571,43 руб. величины прибыли (значения целевой функции). Очевидно, что в данном случае при увеличении значения правой части ограничения значение целевой функции будет возрастать, а при уменьшении — убывать. Насколько же нужно увеличить запас сырья 2, чтобы полностью загрузить все производственные мощности? К сожалению, отчет по устойчивости прямого ответа на этот вопрос не дает. Посмотрим на число в столбце Допустимое увеличение для этого ограничения. Оно равно 6,5. Это значит, что, увеличивая значение правой части ограничения до величины 36,5, мы остаемся в рамках прежнего решения — значения переменных и целевой функции, конечно, будут изменяться, но лимитирующими и нелимитирующими останутся прежние ограничения. Если же значение правой части ограничения будет равно или превысит величину 36,5, то в качестве лимитирующего в игру вступит другое ограничение, которое на данный мом
|