Прямая задача при расчете разветвленных цепей1.2.1 .Симметричная магнитная цепь (рис. 1.10)
Пусть задано значение магнитного потока Ф3, требуется определить МДС w×I намагничивающей обмотки.
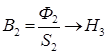 ,  и Н2 определяют по кривой намагничивания. МДС можно определить из уравнения: wI = H3l3 + H2l2.
1.2.2. Несимметричная магнитная цепь (рис. 1.11). Здесь S1=S3 и l3=2l1. Задан поток Ф3, определить МДС w×I.
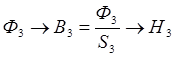 по кривой намагничивания, тогда магнитное напряжение  – по кривой намагничивания, затем Ф1=B1S1 ® Ф2=Ф1+Ф3 ® 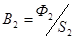 ® H2 – по кривой намагничивания. МДС w×I определим из уравнения w×I = H3l3 + H2l2=Н1l1 + H2l2.
1.2.3. Несимметричная магнитная цепь с двумя намагничивающими обмотками (рис. 1.12). Расчет подобных магнитных цепей производят, используя законы Кирхгофа для магнитных цепей. Перед записью уравнений произвольно намечают направления потоков в стержнях (Ф1, Ф2 и Ф3) и выбирают направления обхода контуров. На рис. 1.12 направления потоков Ф1 и Ф2 приняты совпадающими с МДС w1I1 и w2I2. Условимся со знаком «+» записывать потоки, направленные к узлу а, иначе – со знаком «-».
Со знаком «+» записывать МДС, положительное направление которых совпадает с направлением обхода, иначе – со знаком «-». Для цепи (рис.1.12) можно записать следующие уравнения по законам Кирхгофа:
 
примечание: вместо одного из двух последних уравнений можно записать уравнение для левого контура: Пусть требуется определить МДС w2I2, чтобы магнитная индукция в воздушном зазоре третьего стержня имела заданное значение В0. Решение: 1. S0=S3, имеем В3=В0, тогда поток Ф3=В3S3=В0 S0 2. По кривой намагничивания определим напряженность Н3 3. В4=Ф3 / S4 и по кривой намагничивания определим Н4 4. Напряженность поля в зазоре Н0=В0/m0 5. Из уравнения 1.12 определим напряженность Н2 и по кривой намагничивания находим В2 и поток Ф2=В2S2 6. Из уравнения 1.10 определяется поток Ф1=Ф3 – Ф2 7. Находим индукцию В1=Ф1/ S1 и далее Н1 – по кривой намагничивания 8. Искомое значение w1I1 получаем из уравнения 1.11:
|
В этой цепи l1=l3 и S1=S3. Трехстержневой магнитопровод изготовлен из однородного ферромагнитного материала (кривая намагничивания известна). Магнитные сопротивления стержней 1 и 3 одинаковы. Поток Ф2, возникающий в среднем стержне, разделяется в т. а на две равные части Ф1=Ф3=Ф2 /2.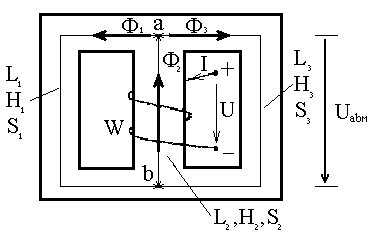
Схема решения:
Со знаком «+» записывать магнитные напряжения, если направление потока на участке цепи совпадет с направлением обхода контура, иначе – со знаком «-».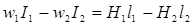
.
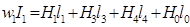