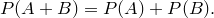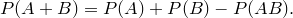Примеры на использование аксиом и теоремы умножения
Определить вероятность поражения цели двумя ракетами, если вероятность поражения каждой равна 0,9. Поражение первой (событие А) и второй ракетой (событие В) есть события независимые.
1.12 Независимые случайные события и их свойства Будем считать, что дано фиксированное вероятностное пространство Определение 1. Два события Вероятность появления события A не меняет вероятности события B. Замечание 1. В том случае, если вероятность одного события, скажем
то есть условная вероятность события Определение 2. Пусть есть семейство (конечное или бесконечное) случайных событий
Определение 3. Пусть есть семейство (конечное или бесконечное) случайных событий
Замечание 2. Совместная независимость, очевидно, влечет попарную независимость. Обратное, вообще говоря, неверно. Пример 1. Пусть брошены три уравновешенные монеты. Определим события следующим образом: · · · Легко проверить, что любые два события из этого набора независимы. Все же три в совокупности зависимы, ибо зная, например, что события Теорема (сложение вероятностей несовместных случайных событий). Вероятность суммы двух несовместных случайных событий
Следствие. Сумма вероятностей противоположных событий равна единице. Теорема. Для произвольных событий
1.13 Независимость случайных событий в совокупности
|



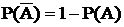 ;
;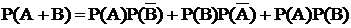
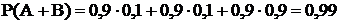 .
. и тогда
и тогда 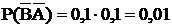
 .
.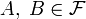 независимы, если
независимы, если , ненулевая, то есть
, ненулевая, то есть  , определение независимости эквивалентно:
, определение независимости эквивалентно: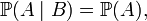
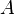 при условии
при условии 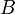 равна безусловной вероятности события
равна безусловной вероятности события  , где
, где 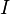 — произвольное индексное множество. Тогда эти события попарно независимы, если любые два события из этого семейства независимы, то есть
— произвольное индексное множество. Тогда эти события попарно независимы, если любые два события из этого семейства независимы, то есть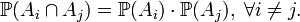
 верно:
верно: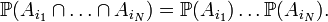
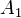 : монеты 1 и 2 упали одной и той же стороной;
: монеты 1 и 2 упали одной и той же стороной; : монеты 2 и 3 упали одной и той же стороной;
: монеты 2 и 3 упали одной и той же стороной; : монеты 1 и 3 упали одной и той же стороной;
: монеты 1 и 3 упали одной и той же стороной; произошли, мы знаем точно, что
произошли, мы знаем точно, что 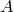 и
и  равна сумме вероятностей этих событий.
равна сумме вероятностей этих событий.