Сигма-алгебра событий.
В теории вероятностей часто возникает необходимость объединять счётные наборы событий и считать событием результат такого объединения. При этом свойства (A3) алгебры оказывается недостаточно: из него не вытекает, что объединение счётной последовательности множеств из алгебры снова принадлежит алгебре. Поэтому разумно наложить более суровые ограничения на класс событий. Определение 11. Множество (S1) (S2) если (S3) если Этого набора аксиом достаточно для замкнутости множества Свойство 2. Свойство (S3) в определении 11 можно заменить на (S4) если Как показывает следующее свойство, всякая Свойство 3. Если Доказательство. Превратим пару
1.4 Статистическое определение вероятности Классическое определение не требует проведения опыта. В то время как реальные прикладные задачи имеют бесконечное число исходов, и классическое определение в этом случае не может дать ответа. Поэтому в таких задачах будем использовать статическое определение вероятностей, которое подсчитывают после проведения эксперимента или опыта. Статической вероятностью w(A) или относительной частотой называют отношение числа благоприятных данному событию исходов к общему числу фактически проведенных испытаний. w (A)= nm Относительная частота события обладает свойством устойчивости: lim n →∞ P (∣ ∣ nm − p ∣ ∣ <ε)=1 (свойство устойчивости относительной частоты)
1.5 Дискретная вероятностная модель. Определение вероятности в рамках дискретной вероятностной модели.
|

 , элементами которого являются подмножества множества
, элементами которого являются подмножества множества 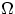 (не обязательно все) называется
(не обязательно все) называется  -алгеброй (
-алгеброй (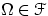 (
( , то
, то 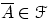 (вместе с любым событием
(вместе с любым событием  ,
,  , то
, то 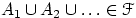 (вместе с любым счётным набором событий
(вместе с любым счётным набором событий  .
. выполняется
выполняется  .
.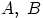 в счётную последовательность событий так:
в счётную последовательность событий так: 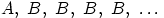 , т.е. положим
, т.е. положим  ,
,  при всех
при всех 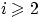 . Объединение
. Объединение 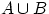 совпадает с объединением всех множеств
совпадает с объединением всех множеств 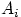 из этой бесконечной последовательности. А так как
из этой бесконечной последовательности. А так как 



