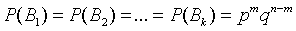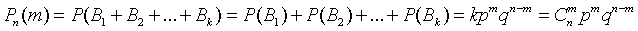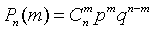Независимость в совокупности.
Если мы рассматриваем произведение трех и более случайных событий, можно говорить о независимости в совокупности: в этом случае вероятность произведения любого количества любых случайных событий равна произведению их вероятностей. Независимость в совокупности является более сильным требованием, чем попарная независимость. Следующий пример показывает, что не всегда из попарной независимости событий следует независимость в совокупности. Замечание. Из взаимной (попарной) независимости не следует независимость в совокупности. Затем мы вычисляем вероятность тройного произведения случайных событий и показываем то, что независимости в совокупности нет (вероятность тройного произведения не равна тройному произведению вероятностей). Определение 3. Пусть есть семейство (конечное или бесконечное) случайных событий
Замечание 2. Совместная независимость, очевидно, влечет попарную независимость. Обратное, вообще говоря, неверно.
1.14 Формула полной вероятности и формула Байеса Формула полной вероятности позволяет вычислить вероятность интересующего события через условные вероятности этого события в предположении неких гипотез, а также вероятностей этих гипотез. Формулировка Пусть дано вероятностное пространство
Замечание Формула полной вероятности также имеет следующую интерпретацию. Пусть
Тогда
т.е. априорная вероятность события равна среднему его апостериорной вероятности. 1.15 Последовательные независимые испытания. Схема Бернулли Предположим, что производится n независимых испытаний, в результате каждого из которых может наступить или не наступить некоторое событие A. Пусть при каждом испытании вероятность наступления события А равна P(A)=p и, следовательно, вероятность противоположного события (ненаступления А) равна Всякую комбинацию, в которую А входит m раз и
Так как в любой другой благоприятной комбинации Вi событие A встречается также m раз, а событие
Формула (13) называется формулой Бернулли *. 1.16 Последовательные независимые испытания до первого «успеха»
|

 . Тогда эти события совместно независимы, если для любого конечного набора этих событий
. Тогда эти события совместно независимы, если для любого конечного набора этих событий  верно:
верно: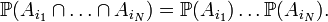
 , и полная группа попарно несовместных событий
, и полная группа попарно несовместных событий 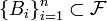 , таких что
, таких что 
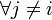
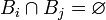
 . Пусть
. Пусть  — интересующее нас событие. Тогда
— интересующее нас событие. Тогда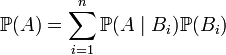 .
. — случайная величина, имеющая распределение
— случайная величина, имеющая распределение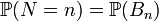 .
.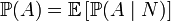 ,
,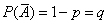 . Определим вероятность Pn(m) того, что событие А произойдет m раз при n испытаниях. При этом заметим, что наступления или ненаступления события А могут чередоваться различным образом. Условимся записывать возможные результаты испытаний в виде комбинаций букв А и
. Определим вероятность Pn(m) того, что событие А произойдет m раз при n испытаниях. При этом заметим, что наступления или ненаступления события А могут чередоваться различным образом. Условимся записывать возможные результаты испытаний в виде комбинаций букв А и  . Например, запись
. Например, запись  означает, что в четырех испытаниях событие осуществилось в 1-м и 4-м случаях и не осуществилось во 2-м и 3-м случаях.
означает, что в четырех испытаниях событие осуществилось в 1-м и 4-м случаях и не осуществилось во 2-м и 3-м случаях.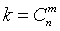

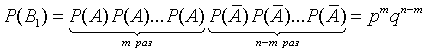
 . Итак
. Итак