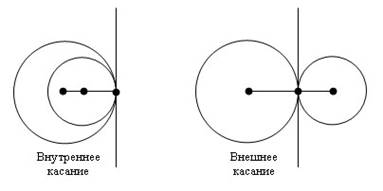
Через точку касания можно провести касательную к одной из окружностей, которая является одновременно и касательной к другой окружности. Касание окружностей бывает внутренним и внешним. Касание называется внутренним, если центры окружностей лежат по одну сторону от касательной. Касание называется внешним, если центры окружностей лежат по разные стороны от касательной
Диаметр окружности, проходящий через середину хорды, не являющейся диаметром, перпендикулярен ей.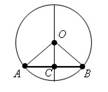 
Уравнение окружности 
Центр в точке A1 (a; b) и радиусом R: (x-a)²+(y-b)²=R² - это уравнение окружности.
Если центр окружности находится в начале координат, т.е. a=0 и b=0, то уравнение окружности принимает вид: x²+y²=R²
Уравнение прямой. Уравнение вида ax + by + c = 0 при условии, что a и b одновременно не равны нулю, задает прямую в плоскости Oxy, и наоборот, уравнение произвольной прямой может быть записано в указанном виде.
