 Выпуклый многоугольник называется правильным, если у него все стороны равны и все углы равны. Сумма углов выпуклого n-угольника равна 180°*(n-2).
Выпуклый многоугольник называется правильным, если у него все стороны равны и все углы равны. Сумма углов выпуклого n-угольника равна 180°*(n-2).
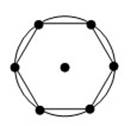
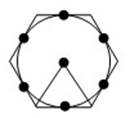 Если все вершины многоугольника лежат на некоторой окружности, то многоугольник называется вписанным в окружность.
Если все вершины многоугольника лежат на некоторой окружности, то многоугольник называется вписанным в окружность.
Если все стороны многоугольника касаются некоторой окружности, то многоугольник называется описанным около окружности.
Описанная и вписанная окружности правильного многоугольника имеют один и тот же центр, который называется центром многоугольника. Центральным углом правильного многоугольника называется угол, под которым видна сторона из его центра.
Вписанная окружность. Центр окружности, вписанной в многоугольник, есть точка равноудаленная от всех сторон этого многоугольника ―точка пересечения биссектрис углов этого многоугольника. Таким образом, в четырехугольник можно вписать окружность, когда суммы его противоположных сторон равны.
Описанная окружность. Центр окружности, вписанной в многоугольник, есть точка равноудаленная от всех вершин этого многоугольника ― точка пересечения серединных перпендикуляров к сторонам этого многоугольника. Около четырехугольника можно описать окружность, когда суммы его противоположных углов равны 180°.
| Площадь.Площадь – это положительная величина, численное значение которой обладает следующими свойствами: 1. Равные фигуры имеют равные площади. 2. Если фигура разбивается на части, то площадь этой фигуры равна сумме площадей ее частей. 3. Площадь квадрата со стороной, равной единице измерения, равна единице.
Площадь четырёхугольника равна половине произведения его диагоналей на синус угла между ними.
| |
 Площадь прямоугольника со сторонами a, b равна: S = a·b. Площадь прямоугольника со сторонами a, b равна: S = a·b.
| |

1. Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне S = a • h. 2. Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними: S=а·b·sinC.
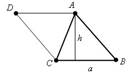 1) Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне: S=
1) Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне: S=  ·a·
·a·  .
.
2) S=  ·a·b·sinC 3) S=
·a·b·sinC 3) S= 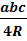 4) S=pr 5) S=
4) S=pr 5) S= 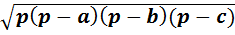
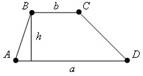 1. Площадь трапеции равна произведению полусумме её оснований на высоту: S=
1. Площадь трапеции равна произведению полусумме её оснований на высоту: S=  ·h
·h

 Выпуклый многоугольник называется правильным, если у него все стороны равны и все углы равны. Сумма углов выпуклого n-угольника равна 180°*(n-2).
Выпуклый многоугольник называется правильным, если у него все стороны равны и все углы равны. Сумма углов выпуклого n-угольника равна 180°*(n-2).
 Если все вершины многоугольника лежат на некоторой окружности, то многоугольник называется вписанным в окружность.
Если все вершины многоугольника лежат на некоторой окружности, то многоугольник называется вписанным в окружность.  Площадь прямоугольника со сторонами a, b равна: S = a·b.
Площадь прямоугольника со сторонами a, b равна: S = a·b.

 1) Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне: S=
1) Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне: S=  ·a·
·a·  .
.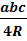 4) S=pr 5) S=
4) S=pr 5) S= 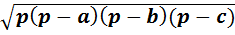
 1. Площадь трапеции равна произведению полусумме её оснований на высоту: S=
1. Площадь трапеции равна произведению полусумме её оснований на высоту: S=  ·h
·h


