Теория эволюции крупномасштабных структур

 

Образование и коллапс протогалактических облаков в представлении художника.

 

Расчётная структура Вселенной по данным Millennium simulation. Отмеченное белой линией расстояние составляет около 141 млн световых лет. Жёлтым обозначена материя, фиолетовым — наблюдаемая лишь косвенно тёмная материя. Каждая жёлтая точка представляет собой одну галактику.

Как показывают данные по реликтовому фону, в момент отделения излучения от вещества Вселенная была фактически однородна, флуктуации вещества были крайне малыми, и это представляет собой значительную проблему. Вторая проблема — ячеистая структура сверхскоплений галактик и одновременно сфероподобная — у скоплений меньших размеров. Любая теория, пытающаяся объяснить происхождение крупномасштабной структуры Вселенной, в обязательном порядке должна решить эти две проблемы (а также верно смоделировать морфологию галактик).

Современная теория формирования крупномасштабной структуры, как впрочем и отдельных галактик, носит названия «иерархическая теория». Суть теории сводится к следующему: вначале галактики были небольшие по размеру (примерно как Магелланово облако), но со временем они сливаются, образуя все большие галактики.

В последние время верность теории поставлена под вопрос и не в малой степени этому способствовал downsizing. Однако в теоретических исследованиях эта теория является доминирующей. Наиболее яркий пример подобного изыскания — Millennium simulation (Millennium run).

Общие положения

Любая теория, так или иначе, предполагает, что все современные образования, начиная от звезд и заканчивая сверхскоплениями, образовались в результате коллапса первоначальных возмущений. Классическим случаем является неустойчивость Джинса, в которой рассматривается идеальная жидкость, которая создает гравитационный потенциал в соответствии с законом Ньютона. В этом случае из уравнений гидродинамики и потенциала получается, что размер возмущения, при котором начинается коллапс, составляет^[82]

,

где u_s — скорость звука в среде, G — гравитационная постоянная, а ρ — плотность невозмущенной среды. Подобное рассмотрение можно провести и на фоне расширяющей Вселенной. Из-за удобства в этом случае рассматривают величину относительной

флуктуации. Тогда классические уравнения примут следующий вид^[82]:

,

,

.

У этой системы уравнений есть только одно решение, которое возрастает со временем. Это уравнение продольных колебаний плотности:

.

Из него, в частности, следует, что нестабильными являются флуктуации точно такого же размера, что и в статическом случае. А растут возмущения линейным образом или слабее, в зависимости от эволюции параметра Хаббла и плотности энергии.

Модель Джинса адекватно описывает коллапс возмущений в нерелятивистской среде, если их размер гораздо меньше текущего горизонта событий (в том числе и для тёмной материи во время радиационно-доминированной стадии). Для противоположных случаев необходимо рассматривать точные релятивистские уравнения. Тензор энергии-импульса идеальной жидкости с учетом малых возмущений плотности

ковариантно сохраняется, из чего следуют уравнения гидродинамики, обобщённые для релятивистского случая. Вместе с уравнениями ОТО они представляют исходную систему уравнений, определяющих эволюцию флуктуаций в космологии на фоне решения Фридмана.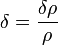
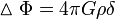