Лекции по ТОЭ/ №16 Представление синусоидальных функций времени комплексными числами.
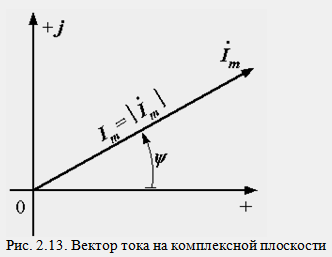
Пусть задано выражение синусоидального тока i=Imsin(ωt+ψ). Как мы видели раньше, этому выражению соответствует вектор, длина которого равна Im, а угол наклона к горизонтальной оси ψ. Если этот вектор изобразить в комплексной плоскости (рис. 2.13), то его можно обозначить комплексным числом Im=Imejψ, которое называется комплексной амплитудой тока.
Комплексное действующее значение тока получается делением последнего выражения на √2 (корень из двух)
Здесь и дальше буквами с точкой над ними (I, U, E) обозначаются комплексные числа, представляющие синусоидальные функции времени. Это ток, напряжение и ЭДС. Комплексные сопротивление и проводимость обозначаются прописными буквами Z и Y, а их модули строчными z и y. Комплексная мощность обозначается буквой S с волнистым значком ˜ (тильда) над ней.
|