Завдання. 1. Виведіть формули для обчислення нарощеної суми за схемою простих позичкових процентів для різних випадків завдання процентних ставок і процентних
1. Виведіть формули для обчислення нарощеної суми за схемою простих позичкових процентів для різних випадків завдання процентних ставок і процентних періодів. 2. Виведіть формули для обчислення нарощеної суми за схемою простих авансових процентів для різних випадків завдання процентних ставок і процентних періодів. 3. Дайте поняття дисконтуванню по простій процентній ставці і напишіть усі можливі формули для позичкових процентів. 4. Проведіть оцінювання дохідності фінансових активів. Методичні рекомендації до практичного заняття Процентна ставка є доходом інвестора від вкладення коштів на визначені цілі і визначений період часу в майбутньому. Процентна ставка – це ціна, яка сплачують інвестору за залучені грошові кошти. Розрізняють номінальна і реальну процентні ставки. Номінальна процентна ставка відображає в грошовому виражені дохід, отриманий з однієї грошової одиниці капіталовкладень
де C – сума інвестованих коштів (суму боргу); k – процентна стака за боргом. Реальна процентна ставка відображає очікувані темпи зростання економіки за визначений період часу і реальний дохід інвестора на вкладені кошти. Реальна процентна ставка дорівнює номінальній ставці за вирахуванням темпів інфляції.
де I – рівень інфляції.
Дохідність депозитних операцій залежить від суми вкладених коштів, способу нарахування процентів та частоти їх нарахування. Якщо на депозитному вкладі розміщена сума, на яку що періоду нараховується проста ставка процентів, загальна сума процентних виплат становитиме:
де кі – процентна ставка в річних, що нараховується в і-му періоді; tі - тривалість і-го періоду, днів. Якщо сума коштів змінюється протягом періоду інвестування, загальна сума процентів визначається так:
де Сі – сума коштів, розміщених на депозиті в і-му періоді. Нарощена сума по вкладу визначається сумою:
У разі нарахування складних процентів по вкладу нарощена сума та загальна сума нарахованих процентів визначається з виразів:
Якщо процентна ставка змінюється протягом періоду інвестування, нарощена за n періодів сума матиме вигляд:
Сума нарахованих процентів при цьому дорівнюватиме:
Якщо проценти нараховуються m раз протягом періоду, нарощення сума визначається так:
Якщо вклади на депозит будуть вноситися регулярно через однакові відрізки часу і на них будуть нараховуватись складні відсотки, можна розрахувати суму депозиту за нарахованими відсотками за весь період його зберігання. Наприклад, якщо щороку в кінці кожного року на протязі n років на депозитний рахунок буде вноситись сума R, а проценти на цю суму будуть нараховуватись за складною річною ставкою і, суми послідовних внесків з процентами, нарахованими на момент закінчення строку зберігання депозиту будуть дорівнювати:
Якщо однакові суми R будуть надходити на депозитний рахунок на початку кожного року, то сума усіх надходжень з нарахованими процентами через n років, буде дорівнювати:
Дохідність операції по обліку векселя (банківсько-дисконтну ставку доходу), як і дохідність будь-якої операції з фінансовими активами на вторинному ринку, може бути розрахована за формулою:
де N - номінаьна вартість векселя; P - ринкова вартість векселя; T- часова база; t – термін погашення векселя, днів. Відповідний дохід називається купонно-еквівалентним доходом. Якщо банк вказує ставку, то за нею можна розрахувати суму P, яка буде сплачена банком власнику векселя при його обліку, та дохід банкуу – дисконт D від обліку векселя:
Контрольні завдання Тестові завдання зазначені після даної теми методичних рекомендацій до самостійної роботи.
|

 (3.1)
(3.1) , (3.2)
, (3.2) (3.3)
(3.3)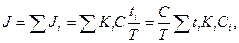 (3.4)
(3.4) (3.5)
(3.5) (3.6)
(3.6) (3.7)
(3.7) (3.8)
(3.8) (3.9)
(3.9) (3.10)
(3.10)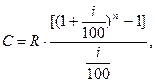 (3.11)
(3.11) (3.12)
(3.12) (3.13)
(3.13)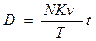 , (3.14)
, (3.14) (3.15)
(3.15)


