Связные графы
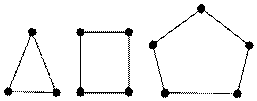
Путем или маршрутом называется конечная последовательность вершин и им инцидентных ребер данного графа, в которой конец каждого ребра, кроме последнего, является началом следующего ребра. Число ребер, входящих в данный путь, называется его длиной. Изолированную вершину можно считать за путь, длина которого равна 0. Путь с началом в вершине A и концом в B вполне можно обозначить последовательностью вершин, через которые он проходит. Например, A – C – D – B. При наличии у графа петель и кратных ребер в эту последовательность вместо прочерков необходимо включать конкретные ребра, по которым проходит путь. Иногда кусок пути, включающий несколько последовательных вершин и ребер будет обозначаться как множество (U, V, W). Расстоянием d(A, B) от вершины A до вершины B называется длина кратчайшего пути с началом A и концом B. Если такого пути не существует, то считают d(A, B)=∞. В одном пути ребра могут повторяться. Цепью называется путь, у которого все ребра различны. Цепь называется простой, если все вершины различны. Простая цепь порядка n обозначается Pn. На рис.25 показаны цепи P2, P3, P4.
Рис. 22 Рис. 23 Цепь называется циклом, когда у нее совпадают первая и последняя вершины. Если такая цепь простая, то цикл называется простым. У простого графа цикл должен содержать не менее трех вершин. На рис. 26 простые циклы порядков 3, 4, 5. Для мульти- и псевдографов циклом может считаться пара кратных ребер или петля.
Доказательство. Рассмотрим для примера Рис. 28. Пусть путь из A в B не является простой цепью. Значит, некоторая вершина C этого пути повторяется минимум дважды, т.е. путь имеет вид: A – U1 – C – U2 – C – U3 – B, где U1, U2, U3 – участки пути от A до C, затем от C до C и от C до B. Если убрать участок U2, можно получить более короткий путь от A до B: A – U1 – C – U3 – B. Продолжая эту процедуру до тех пор пока повторяющихся вершин не останется, можно получить простую цепь от A до B. Граф G называется связным, если для любых двух его вершин A и B существует простая цепь с началом в A и концом в B. В этом случае вершины A и B называются связанными. Для связи двух вершин выполняются следующие свойства: 1. Вершина A связана с A, т.к. существует путь нулевой длины из A в A. 2. Если A связана с B, то B связана с A (пройти путь в обратную сторону). 3. Если A связана с B, а B – с C, то A связана с C (образуем путь из A в C как объединение двух имеющихся путей из A в B и из B в C).
Далее будем рассматривать только простые графы. Дополнением графа G = {P, L; I} называется граф G’ = {P, L’; I’} с теми же вершинами, что и у G, но I’=(P´L)\I.
У простого графа число компонент равно числу его вершин. Две компоненты у графов 1 и 13. На рис 29 у графа G имеется только одна компонента, а у G’ – две. Ребро AB называется мостом графа G, если в графе, полученном после удаления из G ребра AB, вершины A и B оказываются несвязными.
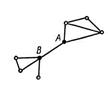
Признаки мостов: 1. Ребро AB является мостом в том и только в том случае, если AB - единственный путь, соединяющий вершины A и B.
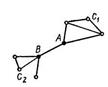
2. Ребро AB является мостом в том и только в том случае, если найдутся две вершины C1 и C2 такие, что каждый путь, соединяющий их, содержит A и B.
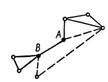
3. Ребро AB является мостом в том и только в том случае, если оно не принадлежит ни одному циклу.
Теорема. Для любого графа либо он связен, либо его дополнение связно. Доказательство. Пусть G = {P, L; I} – несвязный граф и F1 – одна из его компонент, имеющая множество вершин A. Составим подмножество B=P\A, в которое входят все вершины графа G, не принадлежащие F1. Тогда для любой пары вершин A Î A и BÎB дополнительный граф G’ имеет ребро с концами в этих вершинах. Следовательно, произвольная вершина B1 Î B соединена с вершиной A путем длины 1, а произвольная вершина A1 (≠A) тоже соединена с B1 путем длины 1. Отсюда вытекает, что вершины A и A1 из A соединены путем длины 2. Тоже самое верно и для двух любых вершин из B. Следовательно, граф G – связен. Число вершин и ребер графа зависят от числа его компонент. Теорема*. Если у графа G имеется p вершин и q ребер, то у него не менее (p-q) компонент. Если граф G не содержит циклов, то число его компонент ровно (p-q). Теорема. Если у графа G имеется p вершин и k компонент, то число его ребер q удовлетворяет двойному неравенству: Литература: 1. Костюкова Н.И. Графы и их применение. Комбинаторные алгоритмы для программистов: Учебное пособие. – М.: Интернет-Университет Информационных технологий; БИНОМ. Лаборатория знаний, 2007.
|


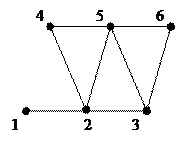

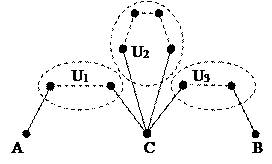 Теорема. Всякий путь из A в B содержит простую цепь с теми же конечными вершинами A и B.
Теорема. Всякий путь из A в B содержит простую цепь с теми же конечными вершинами A и B.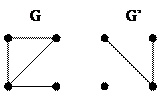 Т.о., «связанность» является отношением эквивалентности на множестве вершин графа. Следовательно, множество всех вершин P можно разделить на непересекающиеся классы, связанных между собой вершин. Подграф графа G, множество вершин которого связано (т.е. совпадает с одним из таких классов), а множество ребер, инцидентных этим вершинам, то же самое, что и в G, называется компонентой графа G (или просто компонентой).
Т.о., «связанность» является отношением эквивалентности на множестве вершин графа. Следовательно, множество всех вершин P можно разделить на непересекающиеся классы, связанных между собой вершин. Подграф графа G, множество вершин которого связано (т.е. совпадает с одним из таких классов), а множество ребер, инцидентных этим вершинам, то же самое, что и в G, называется компонентой графа G (или просто компонентой). Т.о. две вершины графа G смежны тогда и только тогда, когда в G’ они не смежны. На рис 29 показаны граф G и его дополнение G’.
Т.о. две вершины графа G смежны тогда и только тогда, когда в G’ они не смежны. На рис 29 показаны граф G и его дополнение G’.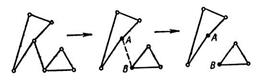
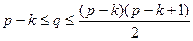 (1).
(1).


