НЕЧЕТКАЯ И ЛИНГВИСТИЧЕСКАЯ ПЕРЕМЕННЫЕ
Итак, нечеткая переменная характеризуется тройкой <a, X, A>, где a - наименование переменной, X - универсальное множество (область определения a), A - нечеткое множество на X, описывающее ограничения (т.е. m A(x)) на значения нечеткой переменной a. Лингвистической переменной назовем переменную, значениями которой являются слова или предложения естественного или искусственного языка. Например, Возраст лингвистическая переменная, если она принимает значения не числовые, а лингвистические, например: молодой, не молодой, очень молодой, старый и т. Д. не 20,21,66,…) Более точно лингвистическая переменная описывается набором <b,T,X,G,M>, где b - название лингвистической переменной; Т - множество ее значений (терм-множество), представляющих собой совокупность ее лингвистических значений. Множество T называется базовым терм-множеством лингвистической переменной; G - синтаксическая процедура, позволяющая оперировать элементами терм-множества T, в частности, генерировать новые термы (значения). Множество TÈ G(T), где G(T) - множество сгенерированных термов, называется расширенным терм-множеством лингвистической переменной; Совокупность значений лингвистической переменной и составляет терм-множество. В нашем примере это перечисление вариантов: молодой, не молодой, очень молодой, старый и т. Д. Это множество может иметь и бесконечное число элементов. М – семантическое правило, которое каждому лигвистическому значению Х ставит в соответствие его смысл, т.е. позволяет сформировать соответствующее нечеткое множество. Замечание. Чтобы избежать большого количества символов символ b используют как для названия самой переменной, так и для всех ее значений; пользуются одним и тем же символом для обозначения нечеткого множества и его названия, например терм " молодой ", являющийся значением лингвистической переменной b = " возраст ", одновременно есть и нечеткое множество М (" молодой "). Пример: Пусть эксперт определяет толщину выпускаемого изделия с помощью понятий " малая толщина ", " средняя толщина " и " большая толщина ", при этом минимальная толщина равна 10 мм, а максимальная - 80 мм. Формализация такого описания может быть проведена с помощью следующей лингвистической переменной <b, T, X, G, M>, где b - толщина изделия; T - {" малая толщина ", " средняя толщина ", " большая толщина "}; X - [10, 80]; G - процедура образования новых термов с помощью связок " и ", " или " и модификаторов типа " очень ", " не ", " слегка " и др. Например: " малая или средняя толщина ", "очень малая толщина " и др.; М - процедура задания на X = [10, 80] нечетких подмножеств А1=" малая толщина ", А2 = "средняя толщина ", А3=" большая толщина ", а также нечетких множеств для термов из G(T) в соответствии с правилами трансляции нечетких связок и модификаторов " и ", " или ", " не ", " очень ", " слегка " и др. операции над нечеткими множествами вида: А Ç В, АÈ В, Пример. Рассмотрим лингвистическую переменную с именем
Графики функций принадлежности термов "холодно", "не очень холодно", "комфортно", "более-менее комфортно", "жарко" и "очень жарко" лингвистической переменной "температура в комнате" показаны на рис.
Оценка эффективности работы представляет собой один из наиболее ответственных этапов в решении целого ряда стратегических задач, характерных для стадии реализации инвестиционной стратегии. Обоснованность принимаемого решения напрямую зависит от того, насколько объективно и всесторонне проведена эта оценка. И спользуются различные методы оценки эффективности работы в условиях риска и неопределенности, к наиболее распространенным из которых следует отнести следующие методы: Ø методы теории игр (критерий максимина, максимакса и др.); Ø построение «дерева решений»; Ø имитационное моделирование по методу Монте-Карло; В качестве примера можно рассмотреть ситуацию, в которой множество допустимых альтернатив представляет собой совокупность всевозможных способов распределения ресурсов, которые ЛПР собирается вложить с целью формирования оптимального инвестиционного портфеля. Очевидно, что, в этом случае, нецелесообразно заранее вводить четкую границу для множества допустимых альтернатив (например, четких ограничений на размер инвестиционного бюджета предприятия в период
|

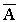 , CON А = А2, DIL А = А0,5 и др.
, CON А = А2, DIL А = А0,5 и др.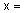 "температура в комнате". Тогда оставшуюся четверку
"температура в комнате". Тогда оставшуюся четверку 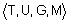 можно определить так:
можно определить так: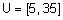 ;
; 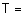 {"холодно", "комфортно", "жарко"} с такими функциями принадлежностями (
{"холодно", "комфортно", "жарко"} с такими функциями принадлежностями (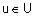 ):
): 


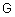 , порождающее новые термы с использованием квантификаторов "не", "очень" и "более-менее";
, порождающее новые термы с использованием квантификаторов "не", "очень" и "более-менее"; 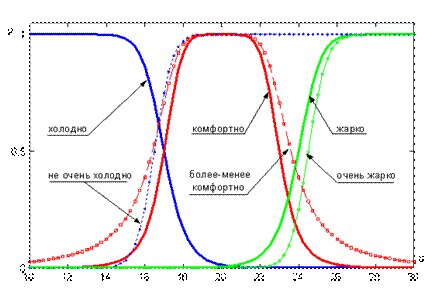
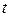 ), поскольку может случиться так, что распределения ресурсов (инвестиционные проекты), незначительно лежащие за этой границей (т.е. вне ограничений), дадут эффект, «перевешивающий» меньшую желательность (например, по размеру инвестиционных затрат) этих распределений для ЛПР. Таким образом, нечеткое описание оказывается более адекватным реальности, чем в определенном смысле произвольно принятое четкое описание задачи.
), поскольку может случиться так, что распределения ресурсов (инвестиционные проекты), незначительно лежащие за этой границей (т.е. вне ограничений), дадут эффект, «перевешивающий» меньшую желательность (например, по размеру инвестиционных затрат) этих распределений для ЛПР. Таким образом, нечеткое описание оказывается более адекватным реальности, чем в определенном смысле произвольно принятое четкое описание задачи.


