Равновесие при массопередаче
Правило фаз. Знание равновесия в процессах массопередачи позволяет установить пределы, до которых могут протекать эти процессы. В основе равновесия лежит известное правило фаз: Ф + С = К + 2, (1) где Ф - число фаз; С - число степеней свободы, т. е. число независимых переменных, значения которых можно произвольно изменять без нарушения числа или вида (состава) фаз в системе; К - число компонентов системы. Правило фаз указывает число параметров, которое можно менять произвольно (в известных пределах) при расчете равновесия в процессах масообмена. Зависимости между независимыми переменными могут быть изображены в плоских координатах в виде так называемых фазовых диаграмм. В расчетах по массопередаче используют диаграммы зависимости давления от концентрации (при t = const), температуры от концентрации (при Р = const) и диаграммы зависимости между равновесными концентрациями фаз, приведенные ниже. Фазовое равновесие. Линия равновесия. Рассмотрим в качестве примера процесс массопередачи, в котором аммиак, представляющий собой распределяемый компонент, поглощается из его смеси с воздухом чистой водой, т. е. ввиду отсутствия равновесия переходит из газовой фазы Фу, где его концентрация равна у, в жидкую фазу Фх, имеющую начальную концентрацию х = 0. С началом растворения аммиака в воде начнется переход части его молекул в обратном направлении со скоростью, пропорциональной концентрации аммиака в воде и на границе раздела фаз. С течением времени скорость перехода аммиака в воду будет снижаться, а скорость обратного перехода возрастать, причем такой двусторонний переход будет продолжаться до тех пор, пока скорости переноса в обоих направлениях не станут равны друг другу. При равенстве скоростей установится динамическое равновесие, при котором не будет происходить видимого перехода вещества из фазы в фазу. При равновесии достигается определенная зависимость между предельными или равновесными концентрациями распределяемого вещества в фазах для данных температуры и давления, при которых осуществляется процесс массопередачи. В условиях равновесия некоторому значению
Отношение концентраций фаз при равновесии называется коэффициентом распределения Конкретный вид законов равновесного распределения различен для разных процессов массопередачи. Так, например, в процессе абсорбции при низких концентрациях распределяемого вещества в исходном растворе равновесие описывается законом Генри для идеальных растворов в процессах ректификации - законом Рауля и т. д. Зная линию равновесия для конкретного процесса и рабочие, т. е. неравновесные, концентрации фаз в соответствующих точках, можно определить направление и движущую силу массопередачи в любой точке аппарата. На основе этих данных может быть рассчитана средняя движущая сила, а по ней - скорость процесса массопередачи.
Зависимость между рабочими концентрациями распределяемого вещества в фазах Рассмотрим схему массообменного аппарата, работающего в режиме идеального вытеснения при противотоке фаз (рис. 2). Пусть в процессе массопередачи из фазы в фазу, например из газовой фазы в жидкую, переходит только один распределяемый компонент (скажем, аммиак). Сверху в аппарат поступает Lн кг/с одной фазы (жидкой), содержащей Тогда материальный баланс по всему веществу
и материальный баланс по распределяемому компоненту
Теперь напишем уравнения материального баланса для части аппарата от его нижнего конца до некоторого произвольного сечения, для которого расходы фаз составляют G и L кг/с, а их текущие концентрации равны Материальный баланс по всему веществу
и материальный баланс по распределяемому компоненту
Решая это уравнение относительно
Уравнение (7) представляет собой уравнение рабочей линии, выражающее связь между рабочими концентрациями распределяемого компонента в фазах для произвольного сечения аппарата. Расходы фаз постоянны по высоте аппарата, например в процессах ректификации, когда числа молей компонентов, которыми обмениваются фазы, равны. В других случаях, если концентрации фаз мало изменяются по высоте аппарата, то расходы фаз по его высоте можно с достаточной для практических целей точностью считать постоянными, т. е. принять L = const и G = const. При этом Lк = L, Gн = G и уравнение (7) приводится к виду
Вводя обозначения
Выражения (8) и (9) являются уравнениями рабочей линии, которыми обычно пользуются при расчетах массообменных процессов. Таким образом, рабочая линия представляет собой прямую, которая наклонена к горизонту под углом, тангенс которого равен А, и отсекает на оси ординат отрезок, равный В. Рабочая линия для всего аппарата ограничена точками с координатами
|

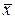 отвечает строго определенная равновесная концентрация в другой фазе, которую обозначим через
отвечает строго определенная равновесная концентрация в другой фазе, которую обозначим через 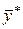 . Соответственно концентрация у отвечает равновесная концентрация
. Соответственно концентрация у отвечает равновесная концентрация 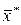 . В самом общем виде связь между концентрациями распределяемого вещества в фазах при равновесии выражается зависимостью:
. В самом общем виде связь между концентрациями распределяемого вещества в фазах при равновесии выражается зависимостью: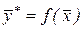 или
или 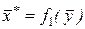 . (2)
. (2)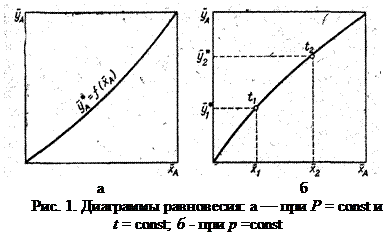 Любая из этих зависимостей изображается графически линией равновесия, которая либо является кривой, как показано на рис. 1, либо в частном случае - прямой линией. На рис. 1, а показана равновесная кривая для системы с компонентами-носителями, выражающая зависимость равновесной концентрации, например в газовой фазе, от концентрации жидкой фазы при Р = const и t = const. На рис. 1, б приведен пример равновесной кривой для процесса ректификации, построенной при Р = const. Каждая точка кривой, как показано на рисунке, соответствует разным температурам (t1, t2 и т. д.).
Любая из этих зависимостей изображается графически линией равновесия, которая либо является кривой, как показано на рис. 1, либо в частном случае - прямой линией. На рис. 1, а показана равновесная кривая для системы с компонентами-носителями, выражающая зависимость равновесной концентрации, например в газовой фазе, от концентрации жидкой фазы при Р = const и t = const. На рис. 1, б приведен пример равновесной кривой для процесса ректификации, построенной при Р = const. Каждая точка кривой, как показано на рисунке, соответствует разным температурам (t1, t2 и т. д.).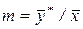 . Для разбавленных растворов линия равновесия близка к прямой, и т является практически величиной постоянной, равной тангенсу угла наклона линии равновесия.
. Для разбавленных растворов линия равновесия близка к прямой, и т является практически величиной постоянной, равной тангенсу угла наклона линии равновесия. Материальный баланс. Рабочая линия. Рабочие концентрации распределяемого вещества не равны равновесным, и в действующих аппаратах никогда не достигают равновесных значений.
Материальный баланс. Рабочая линия. Рабочие концентрации распределяемого вещества не равны равновесным, и в действующих аппаратах никогда не достигают равновесных значений.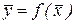 изображается линией, которая носит название рабочей линии процесса. Вид функции
изображается линией, которая носит название рабочей линии процесса. Вид функции 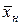 вес. долей распределяемого компонента, а снизу из аппарата удаляется Lк кг/с той же фазы, содержащей
вес. долей распределяемого компонента, а снизу из аппарата удаляется Lк кг/с той же фазы, содержащей  вес. долей распределяемого компонента. Снизу в аппарат поступает
вес. долей распределяемого компонента. Снизу в аппарат поступает  кг/с другой фазы (газовой) концентрацией
кг/с другой фазы (газовой) концентрацией 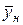 и сверху удаляется
и сверху удаляется 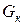 кг/с этой фазы, имеющей концентрацию
кг/с этой фазы, имеющей концентрацию  вес. долей распределяемого компонента.
вес. долей распределяемого компонента.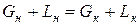 , (3)
, (3) . (4)
. (4) и
и  , (5)
, (5) . (6)
. (6)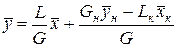 . (7)
. (7)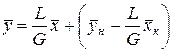 . (8)
. (8) и
и 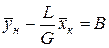 , находим
, находим . (9)
. (9)


