Properties of Definite Integrals
P1. The value of the definite integral of a given function is a real number, depending on its lower and upper limits only, and is independent of the choice of the variable of integration, i.e.
P2. P3. P4. Let P5. Comparison of two integrals If P6. Rules of Integration If (a) (b) Newton – Leibniz formula Comparing the two formulas of the curvilinear trapezoid area, we make the conclusion: if F (x) is primitive for the function f (x) on a segment [ a, b ], then
This is the famous Newton – Leibniz formula. It is valid for any function f (x), which is continuous on a segment [ a, b ]. (i) If then (ii) If Then
|
.
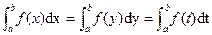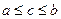, then 
.
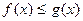
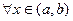, then 
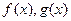are continuous function on 
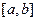then
for some constant k.
.
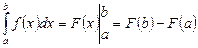
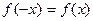(Even Function)
.
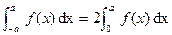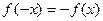(Odd Function)
.
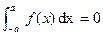