If a continuous curve is defined in rectangular coordinates by the equation  the area of the curvilinear trapezoid bounded by this curve, by two vertical lines at the
the area of the curvilinear trapezoid bounded by this curve, by two vertical lines at the
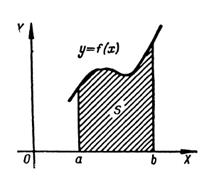
points x=a and x =b and by a segment of the x-axis  , is given by the formula
, is given by the formula
 .
.
In the more general case, if the area S is bounded by two continuous curves 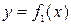 and
and 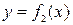 and by two vertical lines x=a and x=b, where
and by two vertical lines x=a and x=b, where  when
when  , we will then have:
, we will then have:
 .
.
If the curve is defined by equations in parametric form 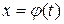 and
and 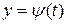 then the area of the curvilinear trapezoid bounded by this curve, by two vertical lines (x=a and x=b), and by a segment of the x-axis is expressed by the integral
then the area of the curvilinear trapezoid bounded by this curve, by two vertical lines (x=a and x=b), and by a segment of the x-axis is expressed by the integral
 ,
,
where 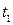 and
and 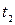 are determined from the equations
are determined from the equations 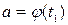 and
and 
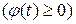 on the interval
on the interval 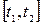 .
.
If a curve is defined in polar coordinates by the equation 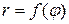 , then the area of the sector AOB (Fig. 2), bounded by an arc of the curve, and by two radius vectors OA and OB,
, then the area of the sector AOB (Fig. 2), bounded by an arc of the curve, and by two radius vectors OA and OB,
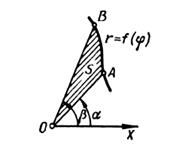
Fig. 2.
which correspond to the values 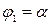 and
and 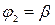 is expressed by the integral
is expressed by the integral
 .
.

 the area of the curvilinear trapezoid bounded by this curve, by two vertical lines at the
the area of the curvilinear trapezoid bounded by this curve, by two vertical lines at the
 , is given by the formula
, is given by the formula .
.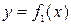 and
and 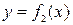 and by two vertical lines x=a and x=b, where
and by two vertical lines x=a and x=b, where  when
when  .
.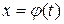 and
and 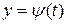 then the area of the curvilinear trapezoid bounded by this curve, by two vertical lines (x=a and x=b), and by a segment of the x-axis is expressed by the integral
then the area of the curvilinear trapezoid bounded by this curve, by two vertical lines (x=a and x=b), and by a segment of the x-axis is expressed by the integral ,
,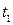 and
and 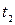 are determined from the equations
are determined from the equations 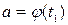 and
and 
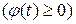 on the interval
on the interval 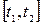 .
.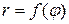 , then the area of the sector AOB (Fig. 2), bounded by an arc of the curve, and by two radius vectors OA and OB,
, then the area of the sector AOB (Fig. 2), bounded by an arc of the curve, and by two radius vectors OA and OB,
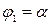 and
and 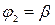 is expressed by the integral
is expressed by the integral .
.


