Complex numbersThe main theorem of algebra. An algebraic equation of the n th degree xn+an-1xn-1+…+a1x+a0=0 has n zeros. (Without a proof.) Example. x3- 1 = 0, (x- 1 )(x2+x+ 1 )=0, x1= 1, x2+x +1=0; D= 1-4=-3,
Definition. The number
i4=i2.i2 =(-1).(-1)=1; i5=i; i6=-i and so on. i.e. is a multiple of 4. Example. Find i35= i32+3 =i3=-i. Definition. A number of the form a=a+bi is called a complex number, where, i is the imaginary unit and а, b are real numbers. Numbers а and bi are called the real and the imaginary parts of a complex number. The following is a geometric interpretation of a complex number
у М(a,b) a=a+bi b 0 x a Each complex number corresponds to a point of the coordinate plane хOу. Each real number is also a complex number with zero imaginary part, i.e. b= 0. For example, 32=32 +0i.
|
- not real numbers.
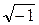is called the imaginary unit and is denoted by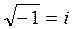 
; i3=-i;
