PRACTICAL CLASS № 7-8.
Rolle's theorem, Lagrange, Cauchy. L'Hopital's rule. Investigation of the function. Extremum of the function. Necessary and sufficient conditions for the existence of an extremum. Convexity, concavity and inflection points. Asymptote. The overall study of design features
Theoretical questions: 1. L’Hospital’s Rule; 2. Monotonic conditions. Extremum of function; 3. Convexity and concavity. Point of inflection; 4. Аsymptotes; 5. Scheme of investigation of function and charting.
Classroom assignments: 1. Find the limits using L'Hospital's rule: 1. 2. Conduct a complete investigation of the functions and construct their graphs: 1. 3. Describe the concavity of the graph of 4.Find 5.Find the domain and all asymptotes of the following function: 6. Find the maximum and minimum values of Homework: Theoretical material: Antiderivative and indefinite integral. Solve problems: 1. Find the limits using L'Hospital's rule: 1. 2. Conduct a complete investigation of the functions and construct their graphs: 1. 3. Find the domain and all asymptotes of the following function: 4. Find the domain and all asymptotes of the following function: 5. Find the maximum and minimum values of 6. Find the maximum and minimum values of
|

 2.
2. 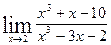 3.
3. 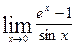 4.
4.  5.
5.  6.
6. 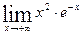 7.
7.  8.
8. 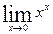 9.
9. 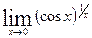
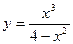 2.
2. 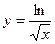
 for
for 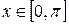 .
. and
and  so that the function
so that the function 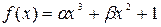 has a point of inflection at
has a point of inflection at  .
. .
. on the interval [0, 5].
on the interval [0, 5].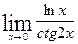 2.
2. 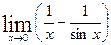 3.
3. 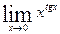 4.
4. 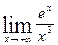
 2.
2. 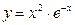 .
.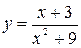 .
. .
. on the interval [-2, 1].
on the interval [-2, 1].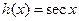 on the interval
on the interval  .
.