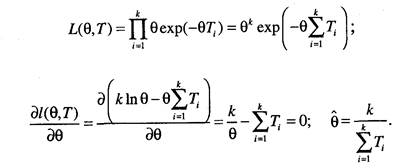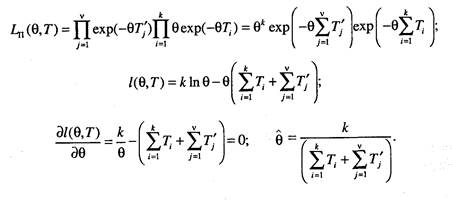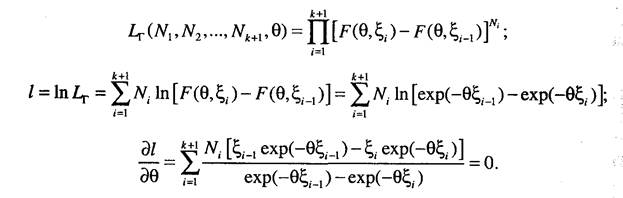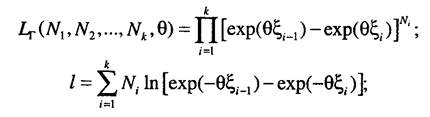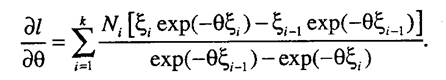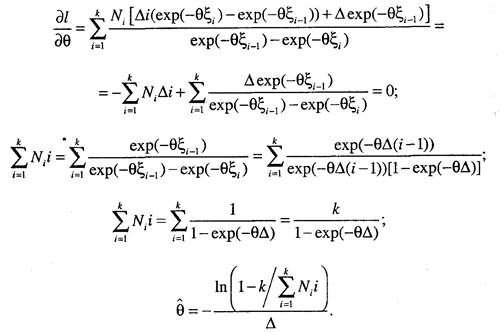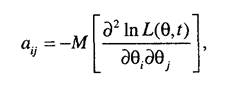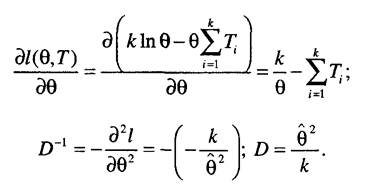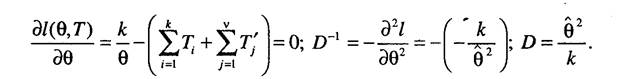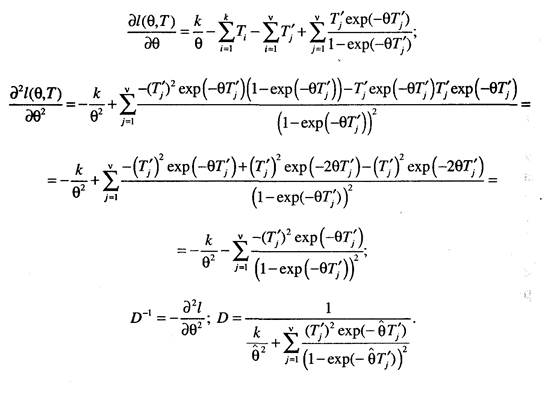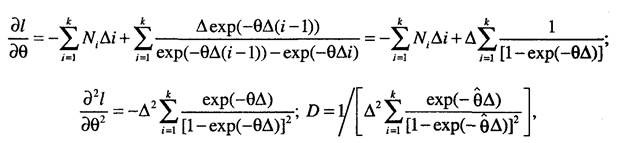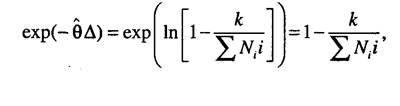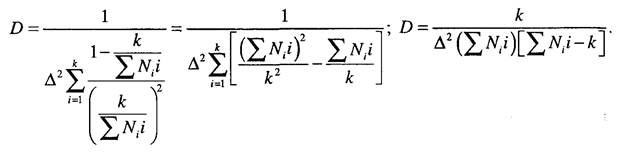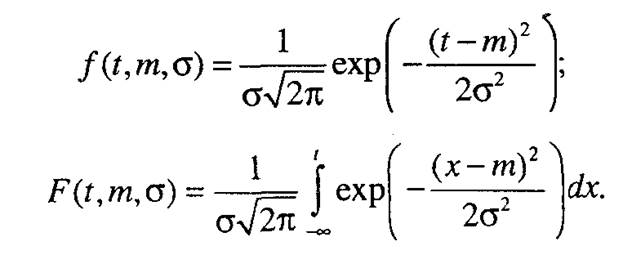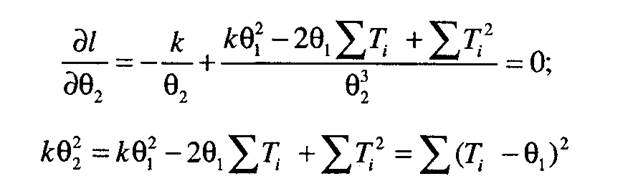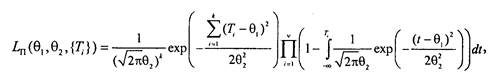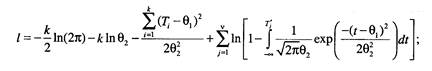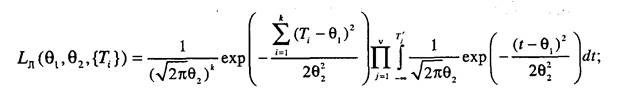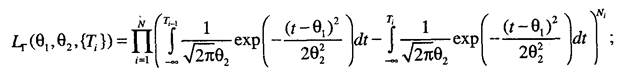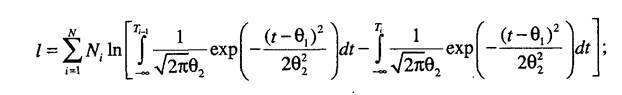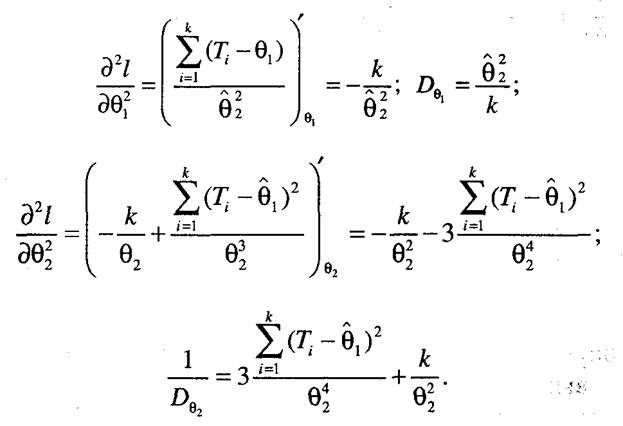Экспоненциальное распределение

1. Для полных наработок имеем:

Таким образом, в данном случае решение получается в явном виде. 2. Для данных, содержащих полные и цензурированные справа на­работки:

Решение так же как и в предыдущем случае получается в явном виде.

3. Для данных, содержащих полные и цензурированные слева нара­ботки:

Данное уравнение в явном виде не имеет представления. Программ­ная реализация решения подобных уравнений требует применения чис­ленных методов.

4. В случае, когда выборка содержит только группированные дан­ные, решение имеет следующий вид:

При равных интервалах цензурирования решение можно представить в следующем виде:

Если представить Ь, =Д/, Ъ,._=Ь.{г- 1), где Д - временной интервал груп­пирования, будем иметь

Приведем результаты определения точности оценки параметра экспоненциального закона распределения.

Дисперсионная матрица для вектора параметров определяется пу­тем транспонирования информационной матрицы, элементы которой имеют вид

в нашем случае оценки одного параметра необходимо определить вто­рую производную по параметру:

В итоге будем иметь следующие результаты. 1. Для полных наработок:

2. Для выборки, содержащей полные и цензурированные справа нара­ботки:

3. Для выборки, содержащей полные и цензурированные слева на­работки:

4. Для группированных данных:

В случае равных интервалов группирования:

имеем в виду, что:

тогда:

Нормальное распределение

Плотность и функция распределения для нормального закона рас­пределения имеют вид:

В данных формулах приняты обозначения: т - математическое ожида­ние; а - среднее квадратическое отклонение. При получении оценок параметров и определении точности в их оценке будем также в каче­стве математического ожидания использовать обозначение 9₍, в каче­стве среднего квадратического отклонения - 9₂. Приведем результаты вычислений.

1. В случае полных наработок имеем:

Производя аналогичные действия для второго параметра, получим

в итоге получаем следующую формулу

2. Для выборок, содержащих полные и цензурированные справа на­работки, функция правдоподобия имеет вид

логарифмическая функция правдоподобия:

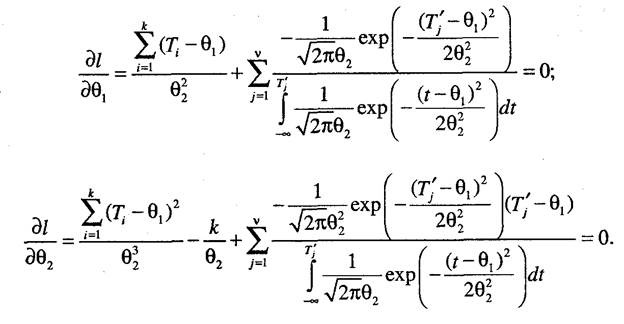
и, наконец, частные производные определяются выражениями

В данном случае результат в явном виде получить не удается, поэтому необходимо решать трансцендентные уравнения.

3. Для выборок, содержащих полные и цензурированные слева' на­работки, функция правдоподобия записывается

логарифмическая функция правдоподобия:

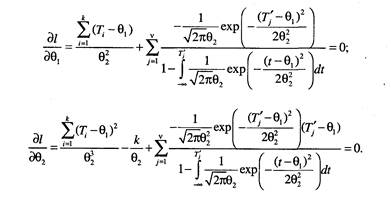
частные производные:

Для выборок, содержащих цензурированные слева наработки, де­лаем тот же вывод, что и в предыдущем случае, а именно, решение необходимо искать численными методами.

4. Для группированных данных итоговые оценки получаются таким образом. Функция правдоподобия:

логарифмическая функция правдоподобия:

производные от нее по параметрам:

Рассмотрим вопрос вычисления точности в полученных оценках. Определим вторые производные для случая, когда имеются в наличии полные наработки.

Для всех остальных типов данных при расчете дисперсии получа­ются результаты, не имеющие представления в явном виде. Поиск ре­шения осуществляется численными методами, поэтому итоговые фор­мулы не приводятся.