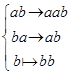Определить, является ли самоприменимым следующий алгоритм W

Разработка вариантов письменного тестирования

Вариант письменного теста (образец).

1. Указать, что будет выведено на экран в результате выполнения следующих операторов программы (программа на языке Паскаль):

 

var a, b, c: integer;

procedure P(a: integer: var b: integer);

begin a:=a+b; b:=b+c; c:=c+a end;

a:=1; b:=2; c:=3; P(c,a); write(a:3, b:3, c:3);

 

2. type T=file of integer;

Описать целочисленную функцию Nmax(f), которая за один просмотр непустого файла f типа Т определяет, сколько раз в этот файл входит его максимальный элемент.

 

 

3. type дерево=­вершина;

вершина=record ключ: integer; лев, прав: дерево end;

Рекурсивно (не используя операторы цикла и перехода) описать процедуру Del(T), которая удаляет (с освобожде­нием памяти) из непустого дерева поиска Т вершину с максимальным ключом.

 

 

4. Нарисовать АВЛ-дерево со следующими свойствами:

а) высота дерева равна h = 4 (пояснение: высота пустого дерева равна 0);

б) у всех вершин, кроме листьев, высота правого поддерева меньше высоты левого поддерева;

в) ключи в вершинах – это целые числа от 1 до n, где n – число вершин в дереве.

 

5. В перемешанной таблице размером L =11 коллизии устраняются методом линейных проб (закрытым хеширова­нием) с помощью первичной функции расстановки I = K mod L и вторичной функции расстановки I =(I + C) mod L, где K – ключ, I – адрес, а С – некоторое целое число от 1 до 10. Пусть в таблицу последовательно заносятся ключи 14, 18, 7, 29, 4, 15, 22 и пусть после вставки ключа 29 таблица приобрела следующий вид:

 

I
K

 

Требуется: либо показать, что такой вид таблицы невозможен ни при каком С, либо указать окончательный вид таблицы (дописать в нее последние три ключа).

 

6. Описать алгоритм Маркова, применимый только к тем словам в алфавите {a,b}, которые задаются следующим определением < прим >: < прим > ::= a {a} | a <прим> b и неприменимый к другим словам в данном алфавите. При этом алгоритм должен содержать не более четырех формул подстановки.

 

--------------------------------------------------------------------------------------------------------

 

Доц. Корухова Л.С.

 

Доц. Пильщиков В.Н.

2.2. Варианты письменного тестирования (10 вариантов)

 

Вариант 1.

 

1. При занесении нового ключа в АВЛ - дерево возникла ситуация (см. рисунок), когда характеристика одной из вершин ½ch½= 2, h -высота поддерева. Указать, в какое поддерево был занесен новый ключ и нарисовать дерево после корректировки характеристик.

 

A

d

B

h

λ

C

h

 

b

g

h-1 h

 

2. Дан алфавит А ={ 0, 1 }. Приведите пример нормального алгоритма в расширенном алфавите А, который не применим ни к одному слову из А ^*, содержит не более трех правил подстановки и самоприменим.

 

3. Пусть T1 и T2 - две машины Тьюринга T1 и T2 в алфавите А={a, b }. Дайте определение эквивалентности T1 и T2.

4. Пусть R - переменная типа char. Что будет напечатано при выполнении следующих операторов программы:… writeln; R:= chr(ord('5')); for R:= '5' to succ(R) do write(R, ','); writeln; …..

5. Приведите описание рекурсивной функции create(h), которая "создает" совершенное дерево заданной высоты h (h >=0) и возвращает в качестве своего значения указатель на созданное дерево типа tree.

6. Укажите, какие числа будут выданы на печать при выполнении следующего фрагмента программы:

var A,B,C,D: integer;

procedure Q (B:integer; var X:integer);

var D:integer;

begin B:=B+20; X:=X+10; D:=C; C:=B+D end;

begin A:=1; B:=2; C:=3; D:=4; Q(A,B); write(A,' ',B,' ',C,' ',D); end.

 

 

Вариант 2.

 

 

Что можно сказать о применимости этого алгоритма к словам из подмножества S слов из (S Í ), содержащим символ 1.

1. Задан нормальный алгоритм T в алфавите A ={0, 1}:
T:

 

 

2. В алфавите А={a, b, c} заданы два алгоритма F, T. Алгоритм F имеет вид : ba à cb, алгоритм R задан машиной Тьюринга (предполагается, что управляющая головка в начале работы указывает на первый символ слова и находится в состоянии q0, qs - состояние останова) Дайте определение эквивалентности двух алгоритмов, заданных в алфавите А.	T:   q0 q1 q2	λ λ,R,qs λ,R,qs λ,R,qs	a a,R,q0 b,L,q2a ,L,qs	b b,R,q1 b,R,q1 c,L,qs	c c,R,q0 c,R,q0 c,L,qs
qs

Эквивалентны ли алгоритмы F и T? Дайте ответ (да/нет) и объясните его.

 

3. type ключ=0..maxint; тело = array[1..40] of char;

 

Каким должно быть описание перемешанной (хешированной) таблицы tab и ее содержимое в момент перед первым занесением ключа, чтобы процедура insert всегда верно включала элемент в таблицу. Функция первичного перемешивания K mod (N+1), где K - ключ, N+1 - простое число. Коллизии ключей разрешаются с помощью списковой памяти переполнения.

 

procedure insert (x: ключ; y: тело);

var q, r: next; return: boolean;

begin q:= tab[ x mod (N+1)]; return:= true;

while (q­.p <> nil) and return do if q­.p­.K = x then

begin return:= false; q­.p­.S:= y end else q:= q­.p;

if return then begin new(r); r­.K:= x; r­.S:= y; r­.p:= nil; q­.p:= r end

end;

 

 

4. Даны две динамические переменные множественного типа, имеющие конкретные значения. Первой переменной присвоить новое значение - множество элементов, принадлежащих второй переменной и не принадлежащих первой. Выписать фрагмент программы (соответствующие описания и действия) для решения этой задачи. Дополнительные переменные не использовать.

 

5. Приведите описание рекурсивной процедуры FP(h, p), которая преобразует непустое дерево Фибоначчи p высоты h (h>=1) в совершенное дерево высоты h, дополняя дерево p вершинами. Считать, что в дереве Фибоначчи для любой нелистовой вершины высота правого поддерева меньше высоты левого.

 

 

6. var h, x, r, y: char; a: record h, x: char; r: record y: char end end;

b: record h: char; r: record e: char end end;

Записать без использования with действия следующего оператора

присоединения:

with a, b, r do begin h:= x; y:= pred(e) end

 

 

Вариант 3.

1. Алфавит А={ 0, 1 }. Напишите нормальный алгоритм Маркова, в котором не более пяти правил подстановки и который применим только к слову 101 и неприменим к другим словам в алфавите А.

 

 

2. Дать описания типов для списков и привести описание процедуры

Transform(L2, L1), осуществляющей преобразование (L2 à L1) заданного двунаправленного списка L2 элементов типа Т (ссылка на предыдущий элемент для первого и ссылка на следующий для последнего – NIL) в однонаправленный список L1. В полученном списке L1 должен быть сохранен порядок следования элементов. Заглавных звеньев нет. Вся освобождаемая память возвращается в список свободной памяти.

 

3. Перемешанная таблица Т[0..12] с функцией первичного перемешивания I = K mod 13 и с функцией вторичного перемешивания I = (I+5) mod 13 (где K-ключ) заполнена ключами: Как выглядит дерево сравнений (дерево поиска), построенное для таких ключей, если ключи поступали в том же порядке, что и в таблицу и не было балансировки и трансформаций дерева? Дайте определение двоичного дерева сравнений

Адрес

Ключ

 

 

4. const N =; {N ≥ 1}

type MASS = array[1..N] of integer;

tree =­node; {указатель на вершину}

node = record key:integer; left,right: tree end;

Не используя операторы цикла и перехода, описать функцию NEWTREE(T), которая по заданному массиву T (типа MASS) из упорядоченных по возрастанию различных ключей строит дерево сравнений высоты O(log₂N) и возвращает ссылку на построенное дерево.

5. Существуют ли два АВЛ-дерева, у которых высота h (0 <= h < =10) одинакова, а число вершин различается на 1024? Приведите ответ (да/нет) и его четкое обоснование. (Замечание. Высота дерева из одного узла равна 1).

6. Дайте определение стека. Приведите возможный вариант описание стека средствами языка программирования. Приведите примеры задач, при решении которых используется стек.

 

Вариант 4.

 

1. Даны нормальные алгоритмы Т1 и Т2:

 

T1: { ab à

T2: { b à a

Выписать нормальный алгоритм Т, эквивалентный композиции этих алгоритмов (ТºТ2(Т1)) и содержащий не более 5 формул подстановки.

 

2. Выписать металингвистические формулы (БНФ), определяющие понятие < прим >;, которое включает в себя те и только те слова в алфавите {c,d}, к которым применим указанный нормальный алгоритм

 

3. Определить, что будет выдано на экран при выполнении следующей программы

program Prog(output);

var a, b, c: integer;

procedure Q(a: integer; var b: integer); begin a:=a+1; b:=b+2; c:=a+b end;

begin a:=1; b:=6; Q(a,a); write(a, b:2, c:2) end;

 

4. Описать функцию NotEmp (t), определяющую, со скольких непустых строк начинается текстовый файл t.

 

5. type дерево=­вершина;

вершина=record элем: integer; лев, прав: дерево end;

список=­звено; звено=record элем: integer; след: список end;

Не используя операторы перехода и цикла, описать процедуру decr (T, L), которая строит список L из всех элементов дерева Т, являющегося деревом поиска. В списке L элементы должны быть упорядочены по убыванию.

6. В перемешанной таблице размером L =11 коллизии устраняются методом линейных проб (закрытым хешированием) с помощью первичной функции расстановки I = K mod L и вторичной функции расстановки I=(I+C) mod L, где K – ключ, I – адрес, а С – некоторое число от 1 до 10. Пусть в таблицу последовательно заносятся ключи 11, 23, 20, 1, 6, 12, 3, 5 и пусть после вставки ключа 6 таблица приобрела следующий вид:

 

I
K

Указать окончательный вид таблицы (дописать в нее последние три ключа).

 

Вариант 5.

 

Определить, является ли самоприменимым следующий алгоритм W

в расширенном алфавите A={a, b}.

W:

Дать ответ (ДА\НЕТ) и привести его обоснование.

 

 

2. Для заданной последовательности ключей 6, 5, 4, 3, 2, 1 - построить АВЛ-дерево в соответствии с алгоритмом построения АВЛ-деревьев. Проставить характеристики в узлах дерева.

 

 

3. Алфавит А={(,), s}. Назовем выражением в алфавите А непустую последовательность символов, сбалансированную по скобкам (каждой открывающей скобке соответствует закрывающая, каждая открывающая скобка предшествует своей закрывающей), внутри скобок может быть любое число символов s. Привести синтаксическую диаграмму для понятия выражение.

 

 

4. Используя нормализованное представление вещественных чисел вида: знак порядка, десятичный порядок (две цифры), знак мантиссы, мантисса

(4 десятичных цифры) и заданные вещественные числа a = +14+2756,

b = +14-2756, c = +01+1000, вычислить

1) r = (a+b)+c

2) p = a+(b+c)

 

 

5. const n = …; k = …; { n, k > 1 }
type M = array [1..n] of 1..maxint;

Описать процедуру SUM(X, S), которая из массива X типа M выделяет не более k таких чисел (они могут повторяться), чтобы их сумма равнялась целому числу S, и печатает набор этих чисел. Если такого набора нет, процедура должна напечатать слово NO.

 

 

6. type список = ­ звено;

звено = record элем: char; след: список end;
Описать рекурсивную процедуру INS(L, E), вставляющую в конец однонаправленного списка L новый элемент E типа char.

 

 

 

Вариант 6.

 

1. Выписать нормальный алгоритм Маркова, применимый только к тем словам из алфавита {r,s}, для которых выполняется хотя бы одно из следующих двух условий:

1) число букв r в слове кратно 3;

2) в слове менее трёх букв s.

В алгоритме должно быть не более четырех правил подстановки.

 

 

2. type список=­звено;

звено=record элем: real; след: список end;

Описать процедуру min2 (L, m1, m2), которая за один просмотр списка L находит два его наименьших элемента и присваивает их параметрам m1 и m2 (m1 < m2). Считать, что в этом списке не менее двух элементов и все элеменьы списка различны.

 

 

3. Что выдаст на экран следующая программа?

program print (output);

var x, y, z: integer;

procedure Q(var x: integer; y: integer; var z: integer);

begin x:=y–1; y:=z–1; z:=x–1 end;

begin x:=2; y:=4; z:=6; Q(z,x,y); writeln(x, y:2, z:2) end.

 

4. Описать целочисленную функцию g(t), которая подсчитывает, сколькими пустыми строками заканчивается текстовый файл t.

 

 

5. type дерево=­вершина;

вершина=record элем: real; лев, прав: дерево end;

Описать рекурсивно (не используя операторы цикла и перехода) функцию neg (T), которая подсчитывает число отрицательных элементов на самом длинном пути (от корня к листу) в непустом двоичном дереве Т. (Если таких путей несколько, выбрать любой из них.)

 

6. Для вставки ключей в перемешанную таблицу T[0..9] используется метод линейных проб (закрытое хеширование) со следующими первичной (h₁) и вторичной (h₂) функциями расстановки: i=h₁(K)=K mod 10 и i=h₂(i)=(i+3) mod 10, где K – ключ и i – индекс. В таблицу занесены следующие ключи:

 

i
K

 

Указать содержимое таблицы Т в случае, когда эти же ключи занесены в неё в обратном порядке.

 

Вариант 7.

 

1. Задан нормальный алгоритм W в алфавите A ={ a, b }:
W:

Что можно сказать о применимости этого алгоритма к словам из подмножества R слов из (R Í ), содержащим букву b?

 

 

2. В алфавите А={a, b, c} заданы два алгоритма F, R. Алгоритм F – нормальный алгоритм в алфавите А, алгоритм R задан машиной Тьюринга (предполагается, что управляющая головка в начале работы указывает на первый символ слова и находится в состоянии q0, qs - состояние останова). Дайте определение эквивалентности двух алгоритмов, заданных в алфавите А. Приведите примеры эквивалентных алгоритмов F и R.

 

 

3. Ответить на вопрос: может ли в дереве Фибоначчи существовать вершина, в левом поддереве которой находится ровно 80 вершин. Ответ обосновать.

 

 

4. Определить, что будет выдано на экран при выполнении следующей программы

program Prog(output);

var a, b, c: integer;

procedure P(var a: integer; b: integer); begin a:=a+1; b:=b+2; c:=a+b end;

begin a:=1; b:=4; P(a,a); write(a:3, b:3, c:5) end;

 

5. Описать функцию Emp (t), определяющую, со скольких пустых строк начинается текстовый файл t.

 

6. Неориентированный граф из N вершин задан матрицей смежности V. Элемент V[i, j] = true, если вершины i и j cвязаны дугой, и false –в противном случае. Не используя оператор цикла и перехода, описать булевскую функцию GRAPH (V, i, j), которая возвращает значение true, если находит хотя бы один путь в графе из вершины i в вершину j (i ≠ j), и печатает вершины (номера), входящие в этот путь. Функция возвращает значение false, если между вершинами i и j нет пути. При построении пути считать, что каждая вершина может встречаться в нем не более одного раза.

 

 

 

Вариант 8.

1. var a, b, c: integer;

procedure P(var a: integer; b: integer);

begin b:=a+b; a:=b+c; c:=c+a end;

Указать, что будет выведено на экран в результате выполнения следующих операторов:

a:=1; b:=2; c:=3; P(c,a); write(a:3, b:3, c:3);

 

2. type T=file of integer;

Описать целочисленную функцию Nmin (f), которая за один просмотр непустого файла f типа Т определяет, сколько раз в этот файл входит его минимальный элемент.

 

3. type дерево=­вершина;

вершина=record ключ: integer; лев, прав: дерево end;

Рекурсивно (не используя операторы цикла и перехода) описать процедуру Del (T), которая удаляет (с освобождением памяти) из непустого дерева поиска Т вершину с минимальным ключом.

 

4. Нарисовать АВЛ-дерево со следующими свойствами:

а) высота дерева равна 4 (пояснение: высота пустого дерева равна 0);

б) у всех вершин, кроме листьев, высота правого поддерева меньше высоты левого поддерева;

в) ключи в вершинах – это целые числа от 1 до n, где n – число вершин в дереве.

 

5. В перемешанной таблице размером L =11 коллизии устраняются методом линейных проб (закрытым хешированием) с помощью первичной функции расстановки I = K mod L и вторичной функции расстановки I =(I + C) mod L, где K – ключ, I – адрес, а С – некоторое целое число от 1 до 10. Пусть в таблицу последовательно заносятся ключи 25, 29, 18, 40, 15, 26, 33 и пусть после вставки ключа 29 таблица приобрела следующий вид:

I
K

Требуется: либо показать (на обратной стороне листа), что такой вид таблицы невозможен ни при каком С, либо указать окончательный вид таблицы (дописать в нее последние три ключа).

 

6. Описать алгоритм Маркова, применимый только к тем словам в алфавите {0,1}, которые задаются следующим определением < слово >: < слово > ::= 0 {0} | 0 <слово> 1 и неприменимый к другим словам в данном алфавите. При этом алгоритм должен содержать не более четырех формул подстановки.

 

Вариант 9.

1. Алфавит А = {a, b}. Напишите нормальный алгоритм Маркова, в котором не более пяти правил подстановки и который применим только к слову aba и неприменим к другим словам в алфавите А.

 

 

2. Дайте определение динамической переменной. Приведите возможный вариант описания динамической переменной и присваивания ей значения. Приведите примеры задач, при решении которых используются динамические переменные.

 

3. Перемешанная таблица Т[0..12] с функцией первичного перемешивания I = K mod 13 и с функцией вторичного перемешивания I = (I+5) mod 13 (где K-ключ) заполнена ключами: Как выглядит дерево сравнений (дерево поиска), построенное для таких ключей, если ключи поступали в том же порядке, что и в таблицу и не было балансировки и трансформаций дерева? Дайте определение двоичного дерева сравнений

Адрес

Ключ

 

 

4. const N =; {N ≥ 1}

type MASS = array[1..N] of integer;

tree =­node; {указатель на вершину}

node = record key:integer; left,right: tree end;

Не используя операторы цикла и перехода, описать функцию SBTREE(T), которая по заданному массиву T (типа MASS), содержащему ключи, строит дерево сравнений высоты O(log₂N) и возвращает ссылку на построенное дерево. В массиве MASS все ключи различны и упорядочены по убыванию.

5. Существуют ли два АВЛ-дерева, у которых высота h (0 <= h < =10) одинакова, а число вершин различается на 512? Приведите ответ (да/нет) и его четкое обоснование. (Замечание. Высота дерева из одного узла равна 1).

6. Дать описания типов для списков и привести описание процедуры CONF(L1, L2), осуществляющей преобразование (L1 à L2) заданного однонаправленного списка L1 элементов типа Т в двунаправленный список L2. В полученном двунаправленном списке L2 должен быть сохранен порядок следования элементов, а также ссылка на предыдущий элемент для первого и ссылка на следующий для последнего – NIL). Заглавных звеньев нет. Вся освобождаемая память возвращается в список свободной памяти.

 

 

Вариант 10.

 

1. Дана последовательность ключей 1, 2, 3, 4, 5, 6, 7, 8, 9. Построить дерево Фибоначчи с такими ключами.

 

 

2. Имеется N населенных пунктов, перенумерованных от 1 до N. Некоторые пары пунктов соединены дорогами. Информация о дорогах представлена матрицей смежности М, элементы которой M[i, j] = 1, если существует путь из пункта i в пункт j, и M[i, j] = 0 в противном случае. Не используя оператор цикла и перехода, написать булевскую функцию PATH (M, i, j), которая возвращает значение true, если между пунктами i и j (i ≠ j) существует путь и печатает номера городов, по которым проходит этот путь. Функция возвращает false, если пути нет. При построении пути считаем, что в населенном пункте бываем не более одного раза.