Линеаризованное уравнение нелинейного элемента
DU=2a I0Di=rDi, r=2a I0.
Полагая, что ic (t) << I0, заменим нелинейную цепь линеаризованной моделью (рис. 2.7). Теперь анализ такой цепи является достаточно простой задачей. Особенностью линеаризованных моделей цепей является то, что постоянные источники в них отсутствуют, поскольку их приращения равны нулю (источник постоянной ЭДС заменяется закороткой, источник постоянного тока - разрывом). Рассмотрим алгоритм линеаризации некоторого абстрактного управляющего элемента (рис. 2.8). Пусть имеются нелинейные зависимости I2=F (Uу, U2), Uу=F (Iу). (2.7)
Проведем линеаризацию относительно режима покоя I20, U20, Uу0. Разложив зависимость (2.7) в ряд Тейлора, получим
Оставляя пока без комментариев физический смысл коэффициентов линеаризованных уравнений S, ri, r11 на основании (2.8) можно построить электрическую линеаризованную модель управляемого элемента (рис. 2.9). Рассмотрим пример использования линеаризованной модели для анализа усилительного устройства, изображенного на рис. 2.10.
За счет источника смещения Есм через управляемый элемент задается ток покоя I20, а под воздействием сигнала Uc (t) этот ток получает полезное приращение DI2 (Uc), которое и требуется определить.
Заменим схему нелинейного устройства на рис. 2.10 линеаризованной моделью этого устройства, для чего управляемый элемент заменим линеаризованной моделью, а источники постоянной ЭДС Есм и Ен закоротим (рис. 2.11). Ясно, что задача определения DI2 (Uc) по такой схеме решается обычным методом электротехники. Поскольку нелинейные зависимости (2.7) для конкретных управляемых элементов чаще всего задаются в виде статических (для постоянного тока) вольт-амперных характеристик, то коэффициенты линеаризованного уравнения могут быть найдены графически. Допустим, что для некоторого элемента зависимость I2=F (Uу, U2)
задана графически (рис. 2.12). Из уравнения (2.8) следует, например, что параметр
Условие DU2=0 означает, что приращения определяют при неизменном значении U20, определяющем режим покоя. Из рис. 2.12 очевиден алгоритм определения S. Аналогично можно определить и другие параметры линеаризованной модели, используя их определения из 2.8 и соответствующие вольт-амперные характеристики.
|

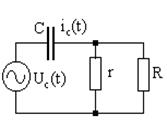 Рис. 2.7. Линеаризован- ная модель цепи по рис. 2.6
Рис. 2.7. Линеаризован- ная модель цепи по рис. 2.6
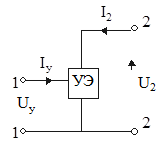 Рис. 2.8. Схема нели- нейного управляемого элемента
Рис. 2.8. Схема нели- нейного управляемого элемента
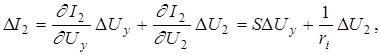 (2.8)
(2.8)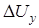 =r11
=r11 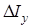 .
.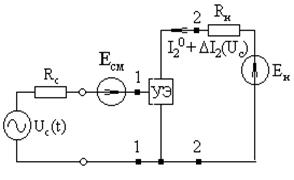 Рис. 2.10. Схема усилительного устройства
Рис. 2.10. Схема усилительного устройства
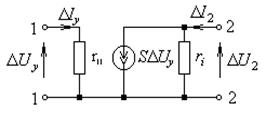 Рис. 2.9. Линеаризованная электрическая модель управляемого элемента
Рис. 2.9. Линеаризованная электрическая модель управляемого элемента
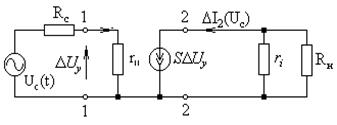 Рис. 2.11. Линеаризованная модель усилительного устройства
Рис. 2.11. Линеаризованная модель усилительного устройства
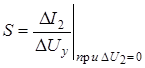 .
.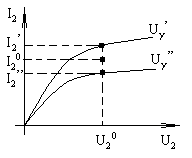
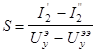 Рис 2.12. Графическое определение коэффициента линеаризованного уравнения
Рис 2.12. Графическое определение коэффициента линеаризованного уравнения



