Частотный анализ линеаризованных цепей
При частотном анализе определяется установившееся значение реакции цепи на гармоническое воздействие x (t) =xm sin w t. Хотя реальные сигналы, действующие в электронных цепях, как правило, не являются гармоническими, тем не менее гармоническое воздействие широко используется как удобный тестовый сигнал. Гармонический сигнал является единственным физически реализуемым сигналом, который при прохождении через линейную цепь не меняет своей формы (меняется лишь амплитуда и появляется фазовый сдвиг, рис. 2.13).
Сохранение формы облегчает анализ (определение реакции), сводя его к определению амплитуды и фазы выходного сигнала. С другой стороны, определяя реакцию цепи на гармонические сигналы разных частот (от низких до высоких), можно определить степень инерционности (быстродействие) цепи, так как максимальная скорость изменения гармонического сигнала во времени пропорциональна частоте x (t) =xm sinw t; При частотном анализе широко используется символический метод (метод комплексных амплитуд), при котором реальный гармонический сигнал x(t)=xm sin w t заменяется символическим (физически не существующим) комплексным экспоненциальным воздействием
Такая замена возможна только для линейной цепи, в которой справедлив принцип суперпозиции и проводится с целью замены дифференциального уравнения цепи алгебраическим. Действительно, дифференцирование и интегрирование (2.9) по времени приводит к следующим очевидным результатам:
то есть к умножению или делению исходной функции на jw. Реакция цепи на символический сигнал ищется в виде
где Представляя в (2.10)
где j (w) - аргумент получим
Таким образом, искомая реакция
Итак, определив Оператор Очень важным является то обстоятельство, что параметры К (w) и j (w)могут быть определены экспериментально для сколько угодно сложной цепи, что широко применяется на практике. Продемонстрируем на простом примере алгоритм частотного анализа. Пусть имеется цепь, связь "вход-выход" которой описывается дифференциальным уравнением
Введем символические значения
подстановка которых в дифференциальное уравнение приводит к равенству
откуда получаем
а окончательно
На основе (2.11) можно построить график АЧХ и ФЧХ (рис. 2.14), по которому определяется реакция цепи на гармоническое воздействие любой частоты (wi). Кроме того, АЧХ позволяет сделать вывод о том, что данная цепь плохо пропускает высокочастотные сигналы, то есть сложный сигнал, проходя через такую цепь, “потеряет” высокочастотные составляющие. На рис. 2.15 показано изменение формы сигнала при прохождении через цепь с АЧХ на рис. 2.14.
|

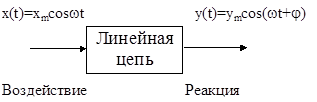 Рис. 2.13. Реакция цепи на гармоническое воздействие
Рис. 2.13. Реакция цепи на гармоническое воздействие
 =w xm cosw t;
=w xm cosw t; 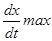 =w xm.
=w xm.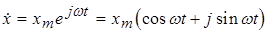 . (2.9)
. (2.9)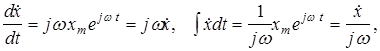
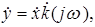 (2.10)
(2.10) - некоторый комплексный оператор.
- некоторый комплексный оператор.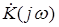 в показательной форме
в показательной форме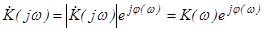 ,
,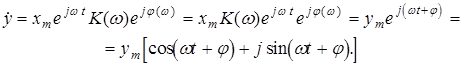

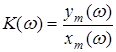 называется амплитудной частотной характеристикой (АЧХ),
называется амплитудной частотной характеристикой (АЧХ), 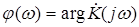 - фазовой частотной характеристикой (ФЧХ).
- фазовой частотной характеристикой (ФЧХ).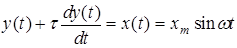 .
.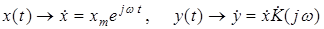 ,
,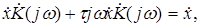
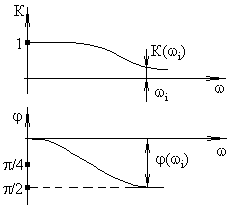 Рис. 2.14. Графики АЧХ и ФЧХ
Рис. 2.14. Графики АЧХ и ФЧХ
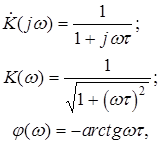 (2.11)
(2.11)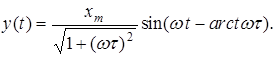
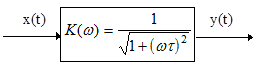
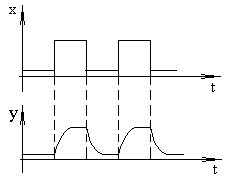 Рис. 2.15. Прохождение импульсного сигнала через цепь с “завалом” АЧХ в области высоких частот
Рис. 2.15. Прохождение импульсного сигнала через цепь с “завалом” АЧХ в области высоких частот



