Статистичекие сети Хопфилда
Если правила изменения состояний для бинарной сети Хопфилда заданы статистически, а не детерминированно, как в уравнении (6.1), то возникает система, имитирующая отжиг. Для ее реализации вводится вероятность изменения веса как функция от величины, на которую выход нейрона OUT превышает его порог. Пусть E k = NETk – qk, где NETk – выход NET нейрона k; q – порог нейрона k, и
(отметьте вероятностную функцию Больцмана в знаменателе), где Т – искусственная температура. В стадии функционирования искусственной температуре Т приписывается большое значение, нейроны устанавливаются в начальном состоянии, определяемом входным вектором, и сети предоставляется возможность искать минимум энергии в соответствии с нижеследующей процедурой: 1. Приписать состоянию каждого нейрона с вероятностью р k значение единица, а с вероятностью 1– р k – нуль. 2. Постепенно уменьшать искусственную температуру и повторять шаг 1, пока не будет достигнуто равновесие.
|

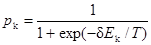 ,
,


