Непрерывные системы
В работе [7] рассмотрены модели с непрерывной активационной функцией F, точнее моделирующей биологический нейрон. В общем случае это S-образная или логистическая функция
где l – коэффициент, определяющий крутизну сигмоидальной функции. Если l велико, F приближается к описанной ранее пороговой функции. Небольшие значения l дают более пологий наклон. Как и для бинарных систем, устойчивость гарантируется, если веса симметричны, т. е. w ij = w ji и w ii = 0 при всех i. Функция энергии, доказывающая устойчивость подобных систем, была сконструирована, но она не рассматривается здесь из-за своего концептуального сходства с дискретным случаем. Интересующиеся читатели могут обратиться к работе [2] для более полного рассмотрения этого важного предмета. Если l велико, непрерывные системы функционируют подобно дискретным бинарным системам, окончательно стабилизируясь со всеми выходами, близкими нулю или единице, т. е. в вершине единичного гиперкуба. С уменьшением l устойчивые точки удаляются от вершин, последовательно исчезая по мере приближения l к нулю. На рис. 6.3 показаны линии энергетических уровней непрерывной системы с двумя нейронами.
|
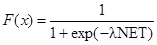, (6.6)
