ОПРЕДЕЛЕНИЕ ГЕОМЕТРИЧЕСКИХ ХАРАКТЕРИСТИК ПОПЕРЕЧНЫХ СЕЧЕНИЙ
ГЕОМЕТРИЯ СЕЧЕНИЙ. ОСНОВНЫЕ ПОНЯТИЯ
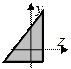
Рассмотрим поперечное сечение произвольной формы. Назначим декартову систему координат. Выделим элементарную площадку dA. Обозначим расстояние от центра тяжести элементарной площадки до оси z через y, до оси y через z, до начала координат через ρ. Тогда геометрические характеристики поперечного сечения можно представить в виде момента площади Площадь (А) – момент нулевого порядка Статический момент площади (S) – момент первого порядка Момент инерции (I) - момент второго порядка. Различают осевые (Iz, Iy), центробежный (Izy) и полярный (Iρ) моменты инерции:
МОМЕНТЫ ИНЕРЦИИ ПРОСТЫХ ФИГУР
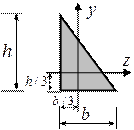
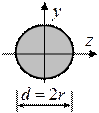
ПРЯМОУГОЛЬНИКПОЛУКРУГРАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК
МОМЕНТЫ ИНЕРЦИИ СОСТАВНЫХ СЕЧЕНИЙ
Для определения геометрических характеристик составных сечений используется следующий подход. Сечение разбивают на несколько простых фигур, моменты инерции которых известны. В центре тяжести каждой фигуры назначают локальную систему координат. Выбирают систему координат относительно которой будет производится расчет. Затем все геометрические характеристики отдельных частей суммируются, а геометрические характеристики отверстий вычитаются. Пример приведен ниже.
назначаем локальные системы координат с началом в центре тяжести каждого прямоугольника. Расчет будем производить в системе координат yz. Ось y - проходит через левую, а ось z - через нижнюю грань составного сечения. При вычислении геометрических характеристик необходимо помнить, что статический момент площади фигуры относительно центральных осей всегда равен нулю, также, как и центробежный момент инерции симметричного сечения.
ИЗМЕНЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПРИ ПОВОРОТЕ ОСЕЙ
Аналогично формулам изменения нормальных и касательных напряжений при ПНС получены зависимости Моменты инерции относительно центральных осей, т.е. осей, проходящих через центр тяжести сечения, называют центральными. Оси, относительно которых центробежный момент инерции обращается в ноль, называют главными и относительно этих осей моменты инерции принимают экстремальное значение. Если главные оси проходят через центр тяжести сечения, то эти оси называют главными центральными, а моменты инерции относительно их – главными центральными моментами инерции. Главные моменты инерции определяют, как Используя приведенный выше материал, вычислим геометрические характеристики сечений, не имеющих осей симметрии и симметричных сечений. ПРИМЕР 1
|

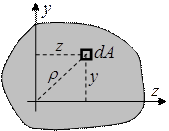 Площадь поперечного сечения является геометрической характеристикой, определяющей напряжение стержня при растяжении-сжатии. При других видах деформации (изгиб, кручение) стержня напряжение зависит от других геометрических характеристик сечения.
Площадь поперечного сечения является геометрической характеристикой, определяющей напряжение стержня при растяжении-сжатии. При других видах деформации (изгиб, кручение) стержня напряжение зависит от других геометрических характеристик сечения.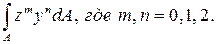
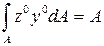 .
.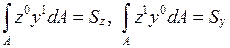 , могут быть положительными, отрицательными, равными нулю. Единицы измерения [см3], [м3]. С помощью статического момента площади определяют координаты центра тяжести сечения yс=Sz/А, zс=Sy/А.
, могут быть положительными, отрицательными, равными нулю. Единицы измерения [см3], [м3]. С помощью статического момента площади определяют координаты центра тяжести сечения yс=Sz/А, zс=Sy/А.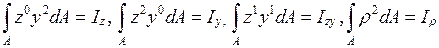 . Осевые моменты инерции (экваториальные моменты) относительно осей координат всегда положительны и отличны от нуля. Центробежный момент инерции может быть положительным, отрицательным, равным нулю. Полярный момент инерции используется для сечений круглой формы, всегда положительный и отличный от нуля. Все моменты инерции измеряются в [см4], [м4].
. Осевые моменты инерции (экваториальные моменты) относительно осей координат всегда положительны и отличны от нуля. Центробежный момент инерции может быть положительным, отрицательным, равным нулю. Полярный момент инерции используется для сечений круглой формы, всегда положительный и отличный от нуля. Все моменты инерции измеряются в [см4], [м4].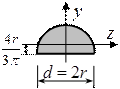
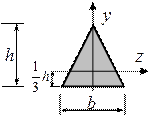
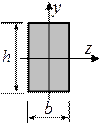
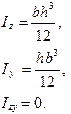
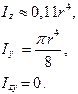
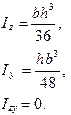

 КРУГПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
КРУГПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК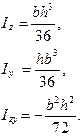
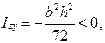
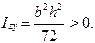


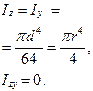
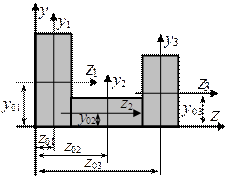 Сечение сложной формы разбиваем на три прямоугольника,
Сечение сложной формы разбиваем на три прямоугольника,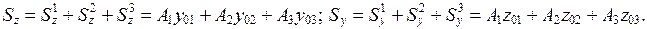
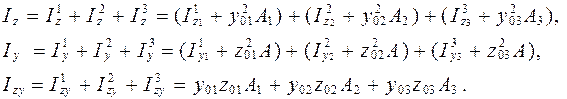
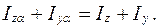
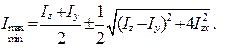 Положение главных осей инерции можно найти с помощью формулы
Положение главных осей инерции можно найти с помощью формулы 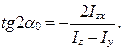
 Определить положение главных центральных осей инерции и вычислить моменты инерции относительно их. Поперечное сечение состоит из двух прокатных профилей: двутавра № 20 и уголка 10/6,3.
Определить положение главных центральных осей инерции и вычислить моменты инерции относительно их. Поперечное сечение состоит из двух прокатных профилей: двутавра № 20 и уголка 10/6,3.


