ПРЕОБРАЗОВАНИЕ НЕКОТОРЫХ НЕЛИНЕЙНЫХ УРАВНЕНИЙ К ЛИНЕЙНОМУ ВИДУ ДЛЯ ИСПОЛЬЗОВАНИЯ В ОДНОФАКТОРНОМ РЕГРЕССИОННОМ АНАЛИЗЕ И ПРОГНОЗИРОВАНИИ
Таблица 4 – Математические выражения прогнозных моделей и их преобразование
| Прогнозная модель и ее графическое представление
| Формулы приведения и расчетные выражения
| Экспоненциальная
 
| система нормальных уравнений 
| |
коэффициенты модели

| Степенная
 
| система нормальных уравнений 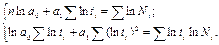
| |
коэффициенты модели

переход от натурального к десятичному логарифму
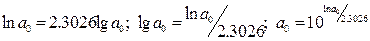
| Логарифмическая
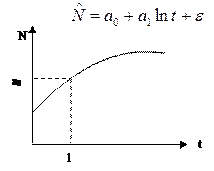
| система нормальных уравнений 
| |
коэффициенты модели

| Окончание таблицы 4
| Прогнозная модель и ее графическое представление
| Формулы приведения и расчетные выражения
| Квадратно-коренная

| система нормальных уравнений 
| |
коэффициенты модели
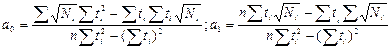
| | Показательная
| система нормальных уравнений 
| |
коэффициенты модели
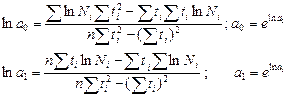
переход от натурального к десятичному логарифму
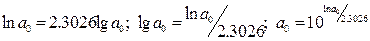 ; ;
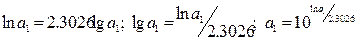
| 
Выполним построение прогнозной модели степенного вида в соответствии с рассмотренной методикой. Исходные данные приведены в таблице 1 задачи. Составим корреляционную таблицу (таблица 5) и определим количественные параметры прогнозной модели.
Воспользовавшись суммарными значениями параметров расчета из таблицы 5, получаем
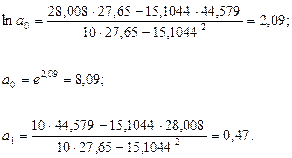
Таблица 5 – Корреляционная таблица (степенная модель)
| Усл. год Ti
| ln T i
| Показатель ln 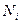
| 
| 
| 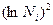
| 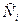
| |
|
| 2,1972246
|
|
| 4,82779584
| 8,09
| |
| 0,69315
| 2,3978953
| 0,4805
| 1,662094
| 5,74990174
| 11,21
| |
| 1,09861
| 2,4849066
| 1,2069
| 2,729949
| 6,17476106
| 13,56
| |
| 1,38629
| 2,8903718
| 1,9218
| 4,006906
| 8,3542489
| 15,52
| |
| 1,60944
| 2,7725887
| 2,5903
| 4,462309
| 7,68724822
| 17,24
| |
| 1,79176
| 2,6390573
| 3,2104
| 4,728556
| 6,96462359
| 18,79
| |
| 1,94591
| 2,944439
| 3,7866
| 5,729614
| 8,6697209
| 20,20
| |
| 2,07944
| 3,0910425
| 4,3241
| 6,427642
| 9,55454345
| 21,51
| |
| 2,19722
| 3,2580965
| 4,8278
| 7,15877
| 10,6151931
| 22,73
| |
| 2,30259
| 3,3322045
| 5,3019
| 7,672684
| 11,1035869
| 23,89
| 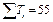
| 15,1044
| 28,008
| 27,65
| 44,579
| 79,702
|
|
 Степенная модель прогнозирования трендовой составляющей изменения объемов среднесуточной переработки транспортной системы имеет вид Степенная модель прогнозирования трендовой составляющей изменения объемов среднесуточной переработки транспортной системы имеет вид
 Прогноз объемов среднесуточной переработки транспортной системы на 20-й год перспективы: Прогноз объемов среднесуточной переработки транспортной системы на 20-й год перспективы:
Степень связи показателей N и t в соответствии со степенной зависимостью (насколько нелинейно изменяются объемы переработки транспортной системы по времени в соответствии с данной зависимостью) определяется с помощью коэффициента корреляции, который равен
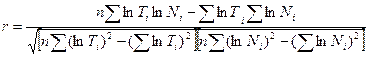
или
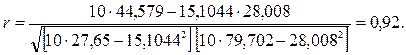
Расчет t–статистики (статистики Стьюдента) и проверка условия значимости коэффициента корреляции показывают, что
 и 6,64>1,86. и 6,64>1,86.
Таким образом, полученное значение коэффициента корреляции значимо отличается от нуля и его значению можно доверять. В тоже время, из таблицы 3 видно, что полученное значение коэффициента корреляции (r =0,92) меньше значения коэффициента корреляции для линейной зависимости (r =0,94), следовательно, она лучше объясняет поведение параметров исследуемого процесса.
Расхождение результатов двух прогнозов
∆ N =46,24 – 33,11=13,13 тыс. т,
что является весомой величиной. В этом случае для целей прогнозирования следует применить линейную зависимость изменения объемов переработки транспортной системы.

Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|

Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...
|

Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...
|

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Статика является частью теоретической механики, изучающей условия, при которых тело находится под действием заданной системы сил...
|
Классификация и основные элементы конструкций теплового оборудования Многообразие способов тепловой обработки продуктов предопределяет широкую номенклатуру тепловых аппаратов...
Именные части речи, их общие и отличительные признаки Именные части речи в русском языке — это имя существительное, имя прилагательное, имя числительное, местоимение...
Интуитивное мышление Мышление — это психический процесс, обеспечивающий познание сущности предметов и явлений и самого субъекта...
|
Методы анализа финансово-хозяйственной деятельности предприятия
Содержанием анализа финансово-хозяйственной деятельности предприятия является глубокое и всестороннее изучение экономической информации о функционировании анализируемого субъекта хозяйствования с целью принятия оптимальных управленческих...
Образование соседних чисел Фрагмент:
Программная задача: показать образование числа 4 и числа 3 друг из друга...
Шрифт зодчего Шрифт зодчего состоит из прописных (заглавных), строчных букв и цифр...
|
|
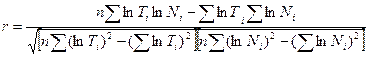




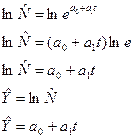



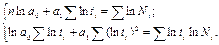


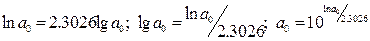
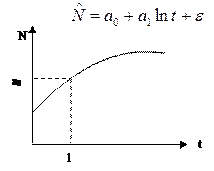

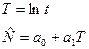





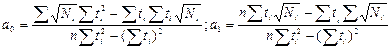
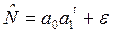


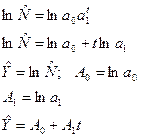
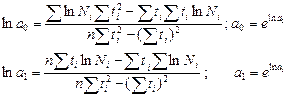
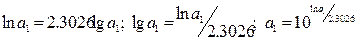
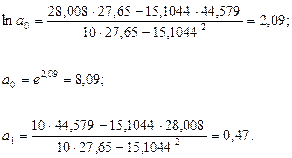
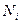


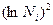
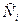
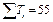
 Степенная модель прогнозирования трендовой составляющей изменения объемов среднесуточной переработки транспортной системы имеет вид
Степенная модель прогнозирования трендовой составляющей изменения объемов среднесуточной переработки транспортной системы имеет вид Прогноз объемов среднесуточной переработки транспортной системы на 20-й год перспективы:
Прогноз объемов среднесуточной переработки транспортной системы на 20-й год перспективы: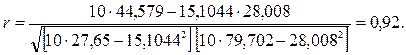
 и 6,64>1,86.
и 6,64>1,86.


