ЗАДАЧА №1
«ПРОГНОЗИРОВАНИЕ ТРАНСПОРТНЫХ ПОТОКОВ С ИСПОЛЬЗОВАНИЕМ ИНТУИТИВНЫХ МЕТОДОВ (КОЛЛЕКТИВНЫЕ ЭКСПЕРТНЫЕ ОЦЕНКИ)»
В задаче №1 требуется по результатам интуитивных прогнозов по исследуемой проблеме (таблица 1) обработать мнения десяти экспертов и дать оценку согласованности их выводов. Рассчитать неопределенность прогноза коллектива. При этом эксперты делают интервальный прогноз, называя минимальную и максимальную границы интервала прогнозируемого показателя на заданную глубину прогнозирования, что является для них предпочтительнее. Таблица 1 (пример)
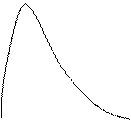
В данной задаче изучается применение интуитивных (эвристических) методов для прогнозирования транспортных потоков на железнодорожном транспорте. Интуитивные методы – это методы, основанные на опросе экспертов (эксперт –«сведущий», высококвалифицированный специалист) по интересуемой организаторов опроса проблеме. При этом эксперты могут делать оценки на основе своих знаний, опыта, интуиции как независимо друг от друга (индивидуальные методы), так и в составе коллектива экспертов (коллективные методы). Интуитивные методы прогнозирования получили широкое распространение благодаря ряду преимуществ: максимальное использование опыта и интуиции специалистов; возможность прогнозирования на длительный период; не требуется установление закономерностей изменения прогнозируемых показателей и описания математических зависимостей (что может быть теоретически затруднено или даже невозможно); способность предсказания резких изменений (скачков или спадов) в работе транспортных систем; не требуется сбор исходных данных. В тоже время максимальное использование этих преимуществ возможно при правильном сочетании интуитивных методов с другими, более точными методами и при их дополнении. Процедура опроса экспертов называется экспертизой. С методологической точки зрения экспертиза организовывается в несколько этапов: – формирование целей и задач экспертизы; – разработка анкет опроса экспертов; – формирование группы экспертов-аналитиков; – формирование коллектива экспертов; – проведение опроса экспертов; – обработка полученных результатов опроса; – выработка заключительного решения. Группа экспертов-аналитиков проводит последние четыре этапа. Для решения задачи используется широко распространенный метод коллективных экспертных оценок. В соответствии с ним для обработки мнений экспертов и расчета неопределенности их прогноза используется метод симметричной аппроксимации. Неопределенность полученных результатов устанавливается на основе вероятностного подхода. При этом рассчитываются такие важнейшие вероятностные характеристики, как математическое ожидание, дисперсия и среднеквадратическое отклонение оценок каждого эксперта и всего коллектива. Расчет выполняется для заранее установленных вероятностных законов распределения оценок экспертов. Наиболее часто используются нормальный закон, равновероятный закон и β -распределение (рисунок 1).
Рисунок 1 – Графики функций плотности распределения для: а) нормального распределения; б) равновероятного распределения; в) β -распределения
Для расчета используются следующие выражения: 1) математическое ожидание прогноза каждого эксперта определяется на основе представленных в таблице 1 нижней и верхней оценок прогнозируемого показателя: для нормального и равновероятного законов
для β -распределения
2) дисперсия оценок каждого эксперта для нормального закона
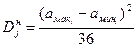 , тр.ед.2; , тр.ед.2;
для равновероятного закона
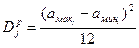 , тр.ед.2; , тр.ед.2;
для β -распределения
 , тр.ед.2 , тр.ед.2
Дисперсия является очень важной величиной, так как позволяет установить уровень компетентности экспертов, степень объективности и другие качественные характеристики.
3) коэффициент вариации оценок каждого эксперта
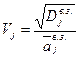 . .
Это означает, что эксперт имеет допустимый уровень разброса верхних и нижних оценок и его мнение может быть учтено в прогнозе всего коллектива экспертов. В противном случае эксперт подлежит исключению из коллектива экспертов и процедура опроса повторяется. Вместо выбывшего могут включаться новые эксперты. Для удобства выполнения анализа, все вычисления сводят в итоговую таблицу (таблица 2).
Таблица 2 – Результаты обработки оценок экспертов
При достаточной компетентности всех экспертов в коллективе рассчитывают параметры коллективного прогноза: математическое ожидание мнений экспертов, дисперсия мнений в коллективе, коэффициент вариации мнений экспертов в коллективе и коэффициент меры расхождения мнений экспертов в коллективе. Последние два коэффициента используются для оценки согласованности мнений экспертов в коллективе. Математическое ожидание (среднеарифметическое значение)
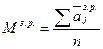 , тр.ед., , тр.ед.,
где n – число экспертов в коллективе. Дисперсия мнений экспертов в коллективе
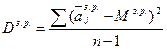 , тр.ед.2 , тр.ед.2
Для оценки согласованности мнений экспертов в коллективе рассчитываются коэффициент вариации мнений экспертов в коллективе V и коэффициент меры расхождения мнений экспертов в коллективе W. Коэффициент вариации мнений экспертов
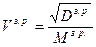 (при (при 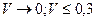 ). ).
Коэффициент меры расхождения мнений экспертов в коллективе
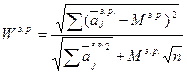 (при (при 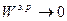 ; ; 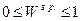 ). ).
Данный коэффициент должен стремиться к «0», что означает полное согласие экспертов по исследуемой проблеме. При
Приемлемыми являются первые три уровня.
Для данных, приведенных в таблице 2, получены следующие результаты (таблица 3).
Таблица 3 – Основные параметры прогноза коллектива экспертов
Данные таблицы 3 показывают, что разброс мнений экспертов не превышает допустимого уровня, степень согласия экспертов в коллективе – сильная. Следовательно, полученному прогнозу можно доверять. Для расчета неопределенности прогноза используется правило «трех сигм». В соответствии с этим правилом интервал неопределенности равен:
 , ,
где σ – среднеквадратическое отклонение мнений экспертов относительно математического ожидания;
М-3σ М М+3σ
Рисунок 2 – Зона неопределенности прогноза
Вывод: 1. Математическое ожидание (прогноз) коллектива экспертов М, тр.ед. 2. Зона неопределенности прогноза (рисунок 2). 3. Степень согласованности мнений экспертов в коллективе (коэффициенты V, W). 4. Уровень разброса оценок каждого эксперта. Качественные характеристики экспертов: «наиболее компетентный эксперт», «наиболее смелый эксперт», «осторожный эксперт», «самый объективный эксперт».
Контрольные вопросы
1. Сущность интуитивных методов прогнозирования транспортных потоков. 2. Кто называется «экспертом»? 3. Что такое неопределенность прогноза? Оценка неопределенности. Сущность метода симметричной аппроксимации. 4. Какая переменная выражает прогноз каждого эксперта? Как определить качественные характеристики экспертов: «наиболее компетентный эксперт», «наиболее смелый эксперт», «осторожный эксперт», «самый объективный эксперт»? 5. Какая переменная выражает прогноз коллектива экспертов? 6. Как оценивается степень согласия экспертов в коллективе? 7. В каких пределах может изменяться коэффициент меры расхождения мнений экспертов? Приведите случай, когда этот коэффициент будет равен «0». 8. Какую информацию «несет» коэффициент вариации мнений экспертов в коллективе? 9.
Рисунок 10. Область применения интуитивных прогнозов. Максимальная глубина прогнозирования. Сравнительная точность прогнозирования.
|

 а) б) в)
а) б) в)
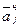
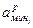
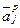
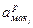
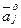
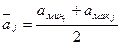 , тр.ед.;
, тр.ед.; , тр.ед.;
, тр.ед.;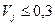 .
.
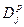
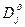
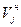
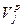
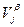
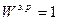 мнения экспертов полностью расходятся. В остальных случаях степень согласия оценивается следующим образом:
мнения экспертов полностью расходятся. В остальных случаях степень согласия оценивается следующим образом: – единодушное мнение;
– единодушное мнение;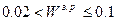 – сильная степень согласия;
– сильная степень согласия;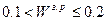 – средняя степень согласия;
– средняя степень согласия;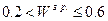 – слабая степень согласия;
– слабая степень согласия;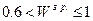 – отсутствие согласованности.
– отсутствие согласованности.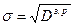 (рисунок 2).
(рисунок 2).
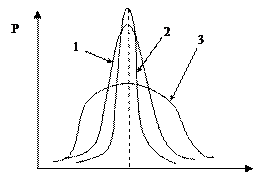 На основе анализа рисунка покажите наиболее предпочтительный из трех прогноз, исходя из вида функции плотности распределения этих прогнозов:
На основе анализа рисунка покажите наиболее предпочтительный из трех прогноз, исходя из вида функции плотности распределения этих прогнозов:


