ЗАДАЧА №3
«ОЦЕНКА КОЛЕБАНИЙ ТРАНСПОРТНЫХ ПОТОКОВ ПРИ РАЗРАБОТКЕ ПРОГНОЗОВ» В задаче №3 требуется определить среднеквадратическое отклонение от среднего значения величины среднесуточного интегрального потока, формируемого из 10 элементарных потоков (таблицы 1, 2). Таблица 1 – Параметры потоков по родам грузов (пример)
Таблица 2 – Коэффициенты взаимной корреляции частных потоков
В соответствии с теорией колебаний транспортных потоков амплитуду колебаний можно оценить с помощью среднеквадратического отклонения значений транспортных потоков относительно их средней величины.
где
Для условий примера результаты расчета колебаний частных потоков приведены в таблице 3. Таблица 3 – Параметры колебаний элементарных (частных) потоков
Далее рассчитывается среднеквадратическое отклонение общего (интегрального) потока, состоящего из 10 элементарных, без учета взаимной корреляции частных потоков между собой:
 , тр.ед. , тр.ед.
В соответствии с данными таблицы 3, имеем
Однако, учет взаимной корреляции отдельных транспортных потоков позволяет уточнить максимальный размах колебаний интегрального потока, и, следовательно, более правильно распределять ресурсы и планировать их переработку. Коэффициенты взаимной корреляции принимаются по таблице 2. Например, коэффициент взаимной корреляции между 3 и 5 родами грузов равен r = –0,80. Это означает, что значения 3 и 5 потоков изменяются взаимосвязано друг с другом, однако в противоположных фазах. Среднеквадратическое отклонение общего (интегрального) потока, состоящего из 10 элементарных, с учетом взаимной корреляции частных потоков между собой:
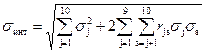 , тр.ед., , тр.ед.,
где r js – коэффициент взаимной корреляции между j и s родами груза. Рассчитывать σинт следует в следующем порядке: Вначале определяется значение суммы
При j=3:
При j=4:
При j=5:
При j=6:
При j=7:
При j=8:
При j=9:
Далее определяется величина слагаемого
Среднеквадратическое отклонение общего (интегрального) потока с учетом взаимной корреляции частных потоков
При сравнении двух переменных σ общ и σ инт возможны следующие случаи: 1. 2. 3. Для условий примера σ общ = 145 тр.ед., σ инт = 100 тр.ед. Следовательно, уменьшение потоков одних грузов частично компенсируются увеличением потоков других (преобладает отрицательная взаимосвязь между частными потоками), что способствует стабилизации интегрального потока. Графическая интерпретация этого процесса показана на рисунке 1.
Рисунок 1 – Эффект компенсации колебаний транспортных потоков
В заключении необходимо рассчитать максимальные и минимальные значения интегрального потока по формулам (с использованием правила «трех сигм»):
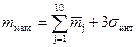 , тр.ед.; , тр.ед.;
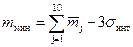 , тр.ед.. , тр.ед..
Эти значения будут характеризовать неопределенность изменения интегрального потока (его верхнюю и нижнюю границы и размах колебаний). Для условий примера
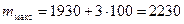 тр.ед.; тр.ед.;
 тр.ед.. тр.ед..
Наибольшую значимость имеет максимальная величина суммарного транспортного потока, т.к. она характеризует уровень потребной пропускной (перерабатывающей) способности, которой должна соответствовать мощность транспортных систем. Вывод: 1. Показать наиболее неопределенный частный поток и наименее неопределенный. 2. Сравнить две переменные σ общ и σ инт и дать обоснованный вывод по результатам сравнения. 3. Привести значения максимального и минимального интегрального потоков. Контрольные вопросы
1. Как оцениваются колебания транспортных потоков на основе вероятностного подхода? 2. В чем выражается необходимость учета колебаний транспортных потоков? 3. Какие существуют теоретические подходы к оценке колебаний транспортных протоков? 4. Что такое коэффициент взаимной корреляции частных транспортных потоков? Покажите на примере его сущность. 5. Почему необходимо учитывать взаимную корреляцию транспортных потоков при оценке их колебаний? 6. Как происходит компенсация колебаний транспортных потоков (рисунок)?
Рисунок
7. Как происходит резонанс колебаний транспортных потоков (рисунок)?
Рисунок 8. Что такое неопределенность изменения транспортного потока? 9. Для чего определяется максимальный транспортный поток? 10. Какие потоки будут иметь более устойчивое состояние и меньшую неопределенность: с постоянным значением среднесуточной величины или с небольшими значениями среднесуточных значений?
|

 , тр.ед.,
, тр.ед.,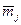 – среднее значение транспортного потока j -го рода груза (таблица 1);
– среднее значение транспортного потока j -го рода груза (таблица 1);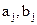 – эмпирические параметры прогнозной модели (таблица 1).
– эмпирические параметры прогнозной модели (таблица 1).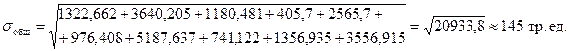
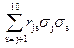 . Расчет ведется по итерациям. Номер итерации соответствует номеру столбца в таблице 2. Например, при j=1
. Расчет ведется по итерациям. Номер итерации соответствует номеру столбца в таблице 2. Например, при j=1 или
или При j=2:
При j=2: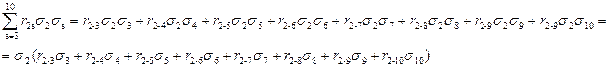 или
или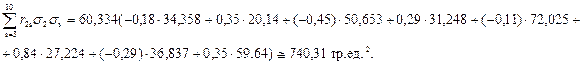
 или
или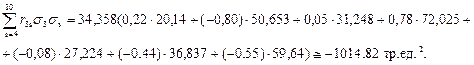
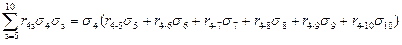 или
или
 или
или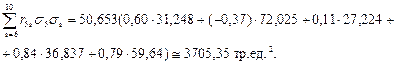
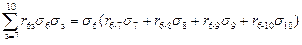 или
или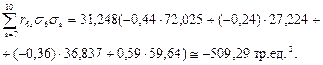
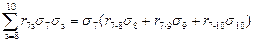 или
или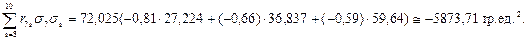
 или
или
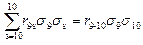 или
или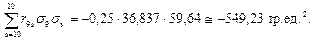
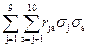 . Для примера
. Для примера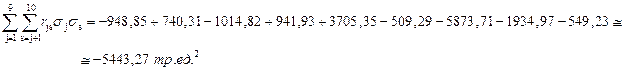
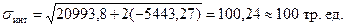
 . Это означает, что преобладает отрицательная корреляция между частными потоками грузов. Предпочтительная ситуация для работы транспортной системы.
. Это означает, что преобладает отрицательная корреляция между частными потоками грузов. Предпочтительная ситуация для работы транспортной системы. . Это означает, что преобладает положительная корреляция между частными потоками грузов. Такая ситуация наиболее неблагоприятная для работы транспортной системы.
. Это означает, что преобладает положительная корреляция между частными потоками грузов. Такая ситуация наиболее неблагоприятная для работы транспортной системы.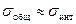 . Это означает, что взаимная корреляция между частными потоками практически отсутствует либо отрицательная взаимосвязь компенсируется положительной.
. Это означает, что взаимная корреляция между частными потоками практически отсутствует либо отрицательная взаимосвязь компенсируется положительной.





