ЗАДАЧА №2. В задаче №2 требуется дать прогноз объемов работы транспортной системы на 20-й год (трендовой составляющей) и оценить значимость и силу связи параметров при
«ПРОГНОЗИРОВАНИЕ ТРЕНДА ТРАНСПОРТНЫХ ПОТОКОВ С ПОМОЩЬЮ ЛИНЕАРИЗОВАННЫХ РЕГРЕССИОННЫХ МОДЕЛЕЙ»
В задаче №2 требуется дать прогноз объемов работы транспортной системы на 20-й год (трендовой составляющей) и оценить значимость и силу связи параметров при аппроксимации данных таблицы 1 линейным законом. Таблица 1 – Объемы работы транспортной системы
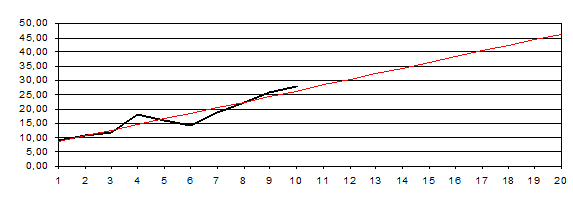
На основе анализа рисунка 1 можно сделать вывод, что среднесуточные объемы переработки транспортной системы растут по годам практически линейно. Следовательно, можно сделать вывод, что наиболее простой и экономичной регрессионной зависимостью, описывающей эту тенденцию, является «линейная» вида:
где а0, а1 – коэффициенты регрессии. С линейной зависимости и следует начинать выбор оптимальной регрессионной зависимости, наиболее адекватной собранным исходным данным. Таким образом, решение задачи сводится к определению правильного положения линии регрессии (зависит от коэффициентов а0, а1), характеризующей тенденцию прошлого и настоящего и экстраполяции ее в будущее (при условии сохранения этой тенденции в будущем). Значения коэффициентов рассчитываются на основе метода наименьших квадратов (МНК). В соответствии с МНК оптимальное положение линии регрессии определяется из условия: где F – функционал рассогласования действительных значений прогнозируемого показателя n – количество точек динамического ряда показателя. Для нахождения минимума функции получают систему нормальных уравнений, из которой и находятся неизвестные а0, а1:
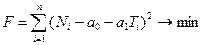 ; ;
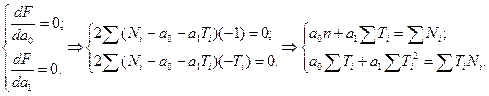
В матричном виде система нормальных уравнений записывается следующим образом:
 . .
Тогда
 , ,
где Δ, Δ0, Δ1 – определители второго порядка, сформированные следующим образом:
 . .
Тогда неизвестные коэффициенты а0, а1
 . .
Для удобства вычислений а0, а1 по формулам (6) составляется корреляционная таблица (таблица 2).
Таблица 2 – Корреляционная таблица
Выполнив вычисления по формулам (6), получаем а0 =6,60; а1 =1,98. Тогда трендовая прогнозная модель, полученная на основе уравнения линейной регрессии
где ε – необъясненная часть исходных данных или ошибка прогнозной модели. С помощью трендовых регрессионных моделей можно выполнять прогнозы с высокой точностью максимальной глубиной до 10 лет. Прогноз объемов среднесуточной переработки транспортной системы на 20-й год перспективы:
Правильность выбора линейной зависимости для прогнозирования среднесуточных объемов переработки транспортной системы устанавливается по коэффициенту корреляции r. Коэффициент корреляции показывает силу линейной связи между зависимым показателем N и независимым интегрированным фактором «время» T. Другими словами, коэффициент корреляции показывает, насколько линейно изменяются объемы переработки транспортной системы по времени. Коэффициент корреляции рассчитывается по формуле

или
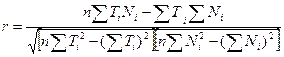 ; ( ; (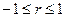 ). ).
Если значения показателя, в основном, увеличиваются и значения независимого фактора увеличиваются, коэффициент корреляции примет знак «+» ( С другой стороны, если значения переменной первого фактора увеличиваются, а второго уменьшаются (или наоборот), коэффициент корреляции примет знак «–» ( Если связь между переменными сильная, коэффициент корреляции будет близок к своим экстремумам. При отсутствии связи коэффициент корреляции близок к «0». В остальных случаях сила связи имеет промежуточные значения: r =0…0,4 – слабая сила связи; r =0,4…0,7 – средняя сила связи; r =0,7…1 – сильная степень связи. В соответствии с формулой (8) для исходных данных, представленных в таблицах 1 и 2
что указывает на весьма сильную линейность тенденции роста объемов переработки. Необходимо проверить это утверждение, оценив значимость коэффициента корреляции. Для этого используется t–статистика (статистика Стьюдента):
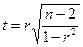 . .
Для условий примера t =8,00 и условие значимости выполняется. Следовательно, значению коэффициента корреляции можно доверять и сильная степень линейности тенденции роста прогнозируемого показателя подтверждается. После завершения процедуры вычислений необходимо проверить также и другие виды регрессионных зависимостей на возможность использования для описания тенденции изменения прогнозируемого показателя (см. приложение к задаче). Для условий примера это могут быть степенная, экспоненциальная, логарифмическая и другие нелинейные зависимости, которые предварительно приводятся к линейному виду. Целесообразно после изучения методики эти вычисления выполнять с помощью компьютерных программ (например, StatGraphics). Лучшим будет считаться тот вид регрессионной зависимости, для которой коэффициент корреляции ближе к экстремуму и значим. Так, согласно выполненным расчетам по приведенной методике в системе StatGraphics, лучшими является следующие модели (таблица 3): Таблица 3 – Данные для сравнения прогнозных моделей
Уравнение наиболее адекватной квадратно-коренная модели:
Вывод: 1. Уравнение линейной регрессии модели прогнозирования 2. Значение прогноза среднесуточной переработки транспортной системы на 20-й условный год. 3. Оценка силы связи параметров прогнозной модели и ее значимость. 4. График изменения динамики прогнозируемого показателя по годам и прогноз на 20-й условный год. На графике показать: исходный динамический ряд, линию регрессии, прогноз, уравнение регрессии.
Контрольные вопросы 1. Область применения формальных методов прогнозирования. Суть методов. 2. Используя график изменения динамики прогнозируемого показателя, постройте графически прогноз для различных периодов упреждения. Рассчитайте для этих же периодов прогноз с помощью уравнения линейной регрессии. Сравните результаты. Объясните расхождение. 3. Что показывает коэффициент корреляции? 4. Для чего оценивается значимость коэффициента корреляции? 5. Что такое «динамический ряд»? 6. Дайте понятие «тренда» прогнозируемого показателя. Какие еще компоненты содержит динамический ряд прогнозируемого показателя? 7. Что выражает переменная ε в прогнозной модели? 8. Что представляет собой «объясненная» часть и «необъясненная» часть исходных данных? 9. Чему равен прогнозный горизонт для трендовых методов прогнозирования? 10. Основное условие МНК. 11. Объясните природу коэффициента корреляции. Как он используется в прогнозировании? 12. Как определяется критическое значение t–статистики?
|

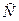 = 6,60 + 1,98 t +ε
= 6,60 + 1,98 t +ε
 ,
,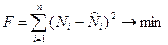 ,
,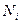 и прогнозных
и прогнозных 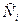 .
.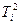

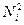
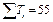



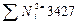
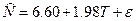 ,
, тыс.т.
тыс.т. ). Такой же знак будет иметь коэффициент корреляции и одновременном уменьшении обоих факторов.
). Такой же знак будет иметь коэффициент корреляции и одновременном уменьшении обоих факторов.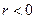 ).
). ,
, , где
, где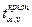 – критическое значение t–статистики, определяемое по таблицам по двум входам: уровню значимости α и числу степеней свободы, равному (n -2). При α =0,05 и n =10 (таблица 1)
– критическое значение t–статистики, определяемое по таблицам по двум входам: уровню значимости α и числу степеней свободы, равному (n -2). При α =0,05 и n =10 (таблица 1) 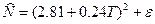 .
.


